今回から、複素関数論を学んでいく。
別の記事(こちら)で既にみているが、複素数の基礎について今一度復習しておくことにする。
複素数の基本
虚数単位i
を用いて、z=x+iyと表されるzを複素数と呼ぶ。x、yはそれぞれ次のようにかく。
$$x=Rez , y=Imz$$
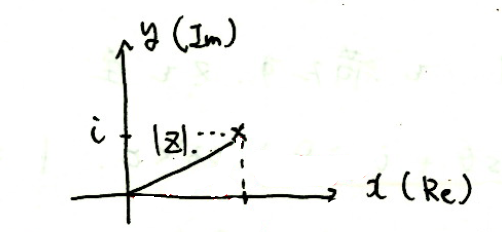
x軸(実軸)とy軸(虚軸)でつくられる平面を複素平面という。原点から点zまでの距離を|z|とかき、
$$|z|=\sqrt{x^2+y^2}=\sqrt{(Rez)^2+(Imz)^2}$$
と計算する。
共役複素数
z=x+iyに対し、次式で与えられる複素数を共役複素数と呼ぶ。
共役複素数について、以下が成り立つ。
$$\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}$$
$$\overline{z_1z_2}=\overline{z_1}・\overline{z_2}$$
$$|z_1+z_2|\le|z_1|+|z_2| (三角不等式)$$
極形式
極座標を用いて複素数を表すことができる。
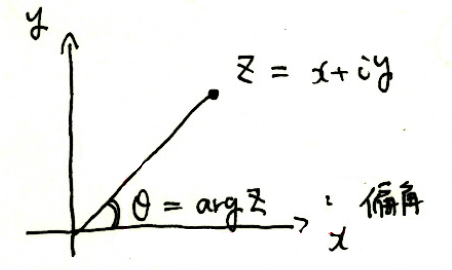
\[
\begin{align*}
z & =x+iy=(r\cos\theta)+i(r\sin\theta) \\
& =r(\cos\theta+i\sin\theta)
\end{align*}
\]
オイラーの公式より、
$$z=re^{i\theta} (極形式)$$
ただし、r=|z|、tanθ=y/xである。θを偏角と呼び、θ=argzとも書く。
極形式で表された複素数z1、z2の積は次のように計算できる。
$$z_1z_2=r_1e^{i\theta_1}・r_2e^{i\theta_2}=r_1r_2e^{i(\theta_1+\theta_2)}$$
よって、偏角については
$$arg(z_1z_2)=arg(z_1)+arg(z_2)$$
となる。
ド・モアブルの定理
複素数のn乗について、以下の等式が成立する。
$$z^n=r^n(\cos n\theta+i\sin n\theta)=r^ne^{in\theta}$$
証明は数学的帰納法による。
この式は、複素数のn乗は単に偏角がn倍されるということを示している。特にr=1の場合、単位円周上を回転することになる。
ド・モアブルの定理を用いた演習問題については以下のリンクを参照。
ド・モアブルの定理による三角関数の倍角公式の証明【理工数学演習】
複素数の極限
と同様である。
$$「任意の\varepsilon>0,あるN>0が存在し、n>Nに対して|z_n-z|<\varepsilon」が成り立つとき$$
$$\lim_{n\to\infty}z_n=z$$
とかく。





