この記事では、材料の変形の基本について学ぶ。
主に金属材料の加工を念頭に話を進めていく。まずは、弾性(elasticity)と塑性(plasticity)の違いを理解しよう。
弾性変形と塑性変形
物体に対して力(荷重)を加えると、変形が生じる。

このときの変形の仕方により、弾性変形と塑性変形に分類することができる。
- 弾性変形:荷重を取り除いたとき、形が元に戻る変形のこと
- 塑性変形:荷重を取り除いても、形が元に戻らない変形のこと
例えば、ばねを引っ張った経験はないだろうか。
ばねを引っ張るとだんだんと伸びていく。ある程度まで引っ張って、手を離すとばねは元の形に戻る。これが弾性変形である。
しかし、強く引っ張りすぎるとばねは伸び切ってしまい、元の形には戻らない。これが塑性変形である。
ばねでなくても、一般の金属材料でこのような現象が起こる。
荷重が小さく、変形量が小さい範囲では弾性変形を生じるが、ある限界を超えると塑性変形して大きな変形が生じる。
ミクロな挙動
ミクロな視点で弾性変形と塑性変形の違いを考えてみよう。
金属は、原子が規則正しく並んだ結晶構造を持っている。原子の集まりからなる金属が変形するということは、原子が動くということである。
金属結合では、原子はある程度の自由度を持って動くことが可能である。

荷重を加えていくと、原子間距離が伸びたり縮んだりする。これは荷重を除くと元の位置に戻るので、弾性変形である。
ある程度であれば原子の位置を変えずに動くことができるが、さらに荷重を加えて変形させようとすると原子の位置が動いてしまう。

このとき、原子がある面に沿ってすべり移動することで大きな変形をすることができる。移動してしまった原子の位置は荷重を除いても元には戻らないので、塑性変形である。
マクロな挙動
次に、日常生活で目にするスケールでの挙動をみてみよう。
金属材料について、様々な材料試験を行うことでその特性を知ることができる。
一軸引張試験をすると、次のような応力-ひずみ曲線を得る。応力\(\sigma\)やひずみ\(\varepsilon\)については別の記事で解説するが、応力≒荷重、ひずみ≒変形量と考えてもらえばいい。
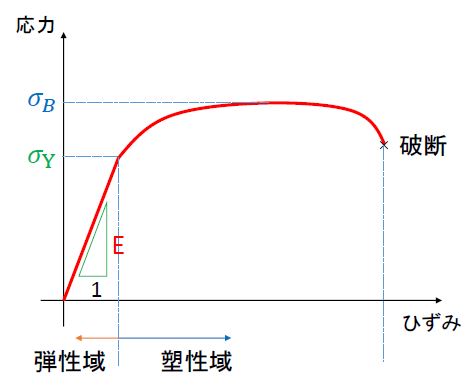
応力とひずみが直線的な関係にある領域が弾性変形、それに続く曲線部が塑性変形をしている部分である。
弾性変形において、直線部分の傾きをヤング率といい、応力とひずみに関して次のフックの法則が成り立つ。
弾性変形から塑性変形に遷移するポイントを弾性限界と呼び、そのときの応力\(\sigma_Y\)を降伏応力という。
塑性変形が進むと、材料は次第に硬くなっていく。これを加工硬化という。
材料が耐えられる最大の引張応力を引張強さという。引張強さを超えると、材料はやがて破断に至る。
種々の金属材料の応力ひずみ曲線
参考までに、いろいろな金属材料に対して引張試験を行った結果を紹介する。
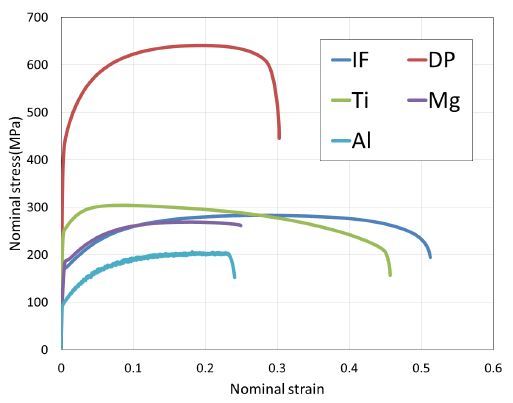
鋼板が二種類(IFとDP)、純チタン、アルミニウム合金、マグネシウム合金の応力ひずみ曲線である。
材料によって、機械的特性が大きく異なることがお分かりいただけることと思う。
このグラフでは見えないが、ヤング率もまた金属により異なる。しかし、弾性変形の領域はいずれの材料でもごく小さなひずみ量のみであることもわかる。


