ここでは、公称応力から真応力、公称ひずみから真ひずみ(対数ひずみ)に換算する方法を解説する。
一軸引張試験から得られる結果は、公称応力-公称ひずみ線図である。一方、数値解析等で取り扱うのは真応力と真ひずみであるので、実験結果と比較するためには両者の変換が必要になる。
手っ取り早く結果だけ知りたいという方のために、先に変換式を示しておく。
\sigma_t=\sigma_n(1+\varepsilon_n) \\
\\
\varepsilon_t=\ln(1+\varepsilon_n)
\end{align*}
以下では、この変換式の導出と、変換する際の注意点について述べる。
下図のように、初期断面積\(A_0\)、初期長さ\(l_0\)の直方体が変形して断面積\(A\)、長さ\(l\)になったとする。
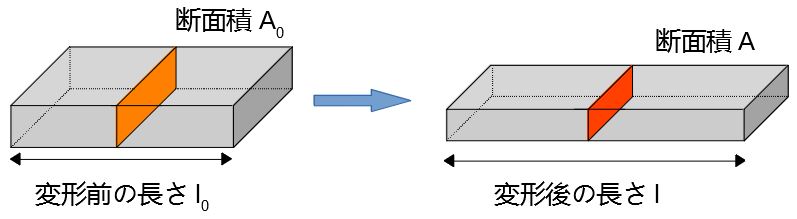
物体は一様に変形、すなわち一部分がくびれて断面積が変化するなどという状態ではないものと考える。
このときの公称応力\(\sigma_n\)、真応力\(\sigma_t\)、公称ひずみ\(\varepsilon_n\)、真ひずみ\(\varepsilon_t\)の定義は以下の通りである。(参考:応力とひずみ)
\begin{cases}
公称応力&:\sigma_n=\frac{F}{A_0} \\
真応力&:\sigma_t=\frac{F}{A} \\
公称ひずみ&:\varepsilon_n=\frac{l-l_0}{l_0} \\
真ひずみ&:\varepsilon_t=\ln\left(\frac{l}{l_0}\right)
\end{cases}
これらの間に成り立つ関係を導こう。
公称ひずみから真ひずみに変換
まずは公称ひずみを真ひずみに換算する。
公称ひずみを式変形すると
\begin{align*}
\varepsilon_n=\frac{l-l_0}{l_0}=\frac{l}{l_0}-1 \\
∴\frac{l}{l_0}=1+\varepsilon_n
\end{align*}
となる。これを真ひずみの定義式に代入すると
$$\varepsilon_t=\ln(1+\varepsilon_n)$$
を得る。これが公称ひずみから真ひずみを求める式である。
公称応力から真応力に変換
次に公称応力を真応力に換算する。
そのためには、体積一定条件を仮定する必要がある。
$$A_0l_0=Al$$
これを用いると、現在の断面積を次のように表現することができる。
$$A=A_0\frac{l_0}{l}$$
さて、これを真応力の定義式に代入すると
\begin{align*}
\sigma_t&=\frac{F}{A} \\
&=\frac{F}{A_0}\frac{l}{l_0} \\
&=\sigma_n(1+\varepsilon_n)
\end{align*}
となる。公称応力と公称ひずみから真応力を得ることができる。
さて、この変換式を用いる際には次のことに注意が必要である。
導出にあたって、変形の一様性を仮定した。つまり変形が不均一な領域ではこの変換式は成り立たない。
したがって、この変換を行うことができるのは一様変形をしている領域に限られることに留意しておこう。
例えば、n乗硬化則に従う材料であれば、引張強さに達するまで一様変形することを示すことができる。別記事で解説予定。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]


