この記事では、変位とひずみの関係式を導出する。
垂直ひずみ、せん断ひずみの定義については既に別の記事で述べた。
[mathjax] ここでは、工学的によく用いられる応力とひずみの定義、計算方法について解説する。 応力やひずみには用途に応じて様々な種類がある。 以下では、垂直応力・ひずみとせん断応力・ひずみの定義、[…]
ここでは、面素の変形に基づいて各ひずみ成分の式を求め、ひずみテンソルを定義する。工学的せん断ひずみとせん断ひずみの違いに特に注意してほしい。
ひずみ-変位関係式
簡単のため、二次元で考えよう。
物体の内部に、幅が\(dx\)で高さが\(dy\)の微小な長方形を考える。変形後にはこの長方形がひずんで下図の赤い四角形になったとする。
実際には、伸び縮みや角度変化のほかにも形状変化を伴わない剛体変位が含まれるが、ここでは原点にオフセットしたものとする。
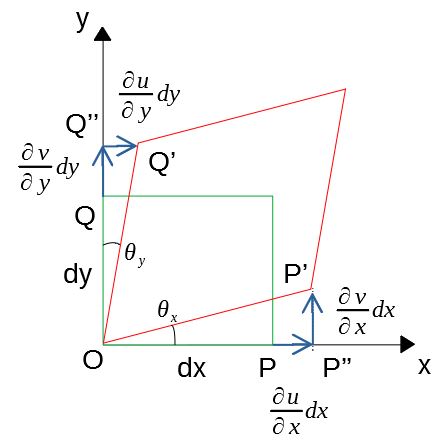
\(x\)方向の変位を\(u(x)\)、\(y\)方向の変位を\(v(y)\)とする。
上図を参考にして、\(x\)方向の垂直ひずみは
\begin{align*}
\varepsilon_{x}&=\frac{OP^{\prime\prime}-OP}{OP} \\
&=\frac{\left(dx+\frac{\partial u}{\partial x}dx\right)-dx}{dx} \\
&=\frac{\partial u}{\partial x}
\end{align*}
と表される。同様に、\(y\)方向については
$$\varepsilon_{y}=\frac{\partial v}{\partial y}$$
である。
次に、せん断ひずみについて考えよう。角度変化が微小であるとすれば、三角関数による近似が可能である。
工学的せん断ひずみ\(\gamma_{xy}\)は、角度変化の和として
\begin{align*}
\gamma_{xy}&=\theta_x+\theta_y \\
&=\frac{P^{\prime}P^{\prime\prime}}{OP^{\prime\prime}}+\frac{Q^{\prime}Q^{\prime\prime}}{OQ^{\prime\prime}} \\
&=\frac{\frac{\partial v}{\partial x}dx}{dx+\frac{\partial u}{\partial x}dx} \\
&≃\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}
\end{align*}
で表される。
この定義は、\(x\)面の\(y\)方向の変化と\(y\)面の\(x\)方向の変化を合わせたものである。
これを均等に2つに振り分けた量として定義されるのがせん断ひずみであり、以下で表す。
\begin{cases}
\varepsilon_{xy}=\varepsilon_{yx}=\displaystyle\frac{\gamma_{xy}}{2} \\
\varepsilon_{yz}=\varepsilon_{zy}=\displaystyle\frac{\gamma_{yz}}{2} \\
\varepsilon_{zx}=\varepsilon_{xz}=\displaystyle\frac{\gamma_{zx}}{2}
\end{cases}
以上より、ひずみ-変位の関係式は次のようにまとめられる。
\begin{cases}
\varepsilon_{x}=\displaystyle\frac{\partial u}{\partial x} \\
\varepsilon_{y}=\displaystyle\frac{\partial v}{\partial y} \\
\varepsilon_{z}=\displaystyle\frac{\partial w}{\partial z} \\
\gamma_{xy}=\displaystyle\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y} \\
\gamma_{yz}=\displaystyle\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z} \\
\gamma_{zx}=\displaystyle\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}
\end{cases}
ただし、\(\gamma_{ij}=2\varepsilon_{ij}~~(i\not=j)\)である。
ひずみテンソル
上で定義した垂直ひずみとせん断ひずみ(工学的せん断ひずみではない)を用いると、ひずみ成分は次の式で表すことができる。
$$\varepsilon_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$$
ひずみは二つの添え字を用いて記述される、2階テンソルであることがわかる。
行列の形で表すと
\[
\varepsilon=\varepsilon_{ij}=\left(
\begin{array}{ccc}
\varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz} \\
\varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz} \\
\varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz}
\end{array}
\right)
\]
となる。
上で定義したように\(\varepsilon_{ij}=\varepsilon_{ji}\)なので、ひずみテンソルは対称テンソルである。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]



