この記事では、応力の表し方について解説する。
垂直応力、せん断応力についての簡単な説明は別の記事で既に述べたが、今回はより一般化した応力ベクトル・応力テンソルを取り扱う。
[mathjax] ここでは、工学的によく用いられる応力とひずみの定義、計算方法について解説する。 応力やひずみには用途に応じて様々な種類がある。 以下では、垂直応力・ひずみとせん断応力・ひずみの定義、[…]
応力やひずみは二階テンソルで表され、塑性力学や有限要素法などの応用分野ではテンソルとして扱う必要がある。ここでその概念を理解しておきたい。
応力テンソル
外力が作用している物体の内部に、微小な直方体を考える。
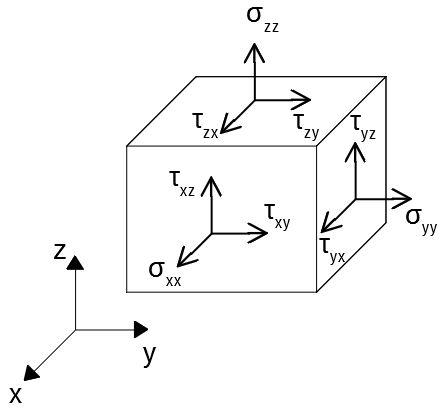
この直方体には、周囲からの力が作用している。
応力は単位面積当たりの力であるので、例えば上図の手前の面に働く力\(\boldsymbol{t}_x\)を応力ベクトルという。このベクトルを、面に垂直(ここでは\(x\)軸)方向の成分と平行(\(y,z\)軸)方向の成分に分解することができる。
成分の表し方を、2つの添え字を用いて次のように定義しよう。
1つ目の添え字は、作用する面を表す。例えば、面の外向き法線方向が\(x\)軸に一致する場合、\(x\)面と呼ぶ。
2つ目の添え字は、作用する方向を表す。
これにより、\(\sigma_{ij}\)は\(i\)面に働く\(j\)方向の単位面積当たりの力を表すことになる。
さて、面と方向の組み合わせから、応力は次の9つの成分を持つことがわかる。
\[
\sigma=\sigma_{ij}=\left(
\begin{array}{ccc}
\sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\
\sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz}
\end{array}
\right)
\]
これが応力テンソルである。
垂直応力を\(\sigma\)、せん断応力を\(\tau\)で表すことから、次のようにも記述される。
\[
\sigma=\left(
\begin{array}{ccc}
\sigma_{x} & \tau_{xy} & \tau_{xz} \\
\tau_{yx} & \sigma_{y} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \sigma_{z}
\end{array}
\right)
\]
実際には、後述するモーメントのつり合いから
$$\sigma_{ij}=\sigma_{ji} すなわち \tau_{xy}=\tau_{yx},\tau_{yz}=\tau_{zy},\tau_{zx}=\tau_{xz}$$
であることがわかる。したがって、ある点の応力は独立な6個の成分により表される。
応力をあえてテンソル表記で表すと、次のように書くことができる。
$$\sigma=\sigma_{ij}(\boldsymbol{e}_i\otimes\boldsymbol{e}_j)$$
ただし\(\boldsymbol{e}_i\)は\(x,y,z\)軸方向の基底ベクトルを表す。
応力ベクトル
応力ベクトル\(\boldsymbol{t}\)は、応力テンソル\(\sigma\)と単位法線ベクトル\(\boldsymbol{n}\)により次式で与えられる。
$$\boldsymbol{t}=\sigma^T\boldsymbol{n}$$
応力テンソルがわかっているとき、任意の面の法線方向を指定すれば、その面に作用する力を知ることができる。
\(x,y,z\)方向に対して書き下して表示すれば
\[
\left(
\begin{array}{c}
t_x \\
t_y \\
t_z
\end{array}
\right)=\left(
\begin{array}{ccc}
\sigma_{xx} & \sigma_{yx} & \sigma_{zx} \\
\sigma_{xy} & \sigma_{yy} & \sigma_{zy} \\
\sigma_{xz} & \sigma_{yz} & \sigma_{zz}
\end{array}
\right)\left(
\begin{array}{c}
n_x \\
n_y \\
n_z
\end{array}
\right)=\left(
\begin{array}{c}
\sigma_{xx}n_x+\sigma_{yx}n_y+\sigma_{zx}n_z \\
\sigma_{xy}n_x+\sigma_{yy}n_y+\sigma_{zy}n_z \\
\sigma_{xz}n_x+\sigma_{yz}n_y+\sigma_{zz}n_z
\end{array}
\right)
\]
となる。
補足:応力テンソルの対称性について
モーメントのつり合いを考えることで、応力が対称性を持つことを示す。
各辺の長さが\(dx,dy,dz\)である直方体について、まず\(z\)面の中心を通る軸周りのモーメントを考えよう。
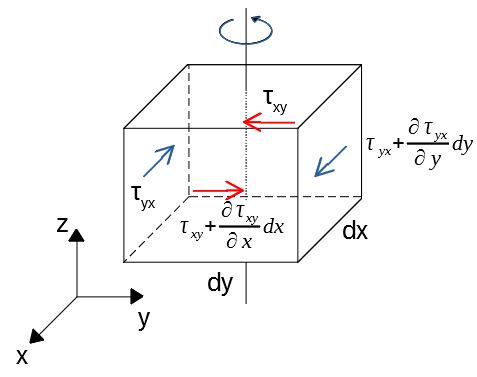
つり合い式は
\begin{align*}
&\tau_{xy}・dy・dz・\frac{dx}{2}+\left(\tau_{xy}+\frac{\partial\tau_{xy}}{\partial x}dx\right)・dy・dz・\frac{dx}{2} \\
&-\tau_{yx}・dx・dz・\frac{dy}{2}-\left(\tau_{yx}+\frac{\partial\tau_{yx}}{\partial y}dy\right)・dx・dz・\frac{dy}{2}=0
\end{align*}
となる。展開して整理すると
\begin{align*}
&\tau_{xy}dydzdx+\frac{\partial\tau_{xy}}{\partial x}dydz\frac{dx^2}{2} \\
&-\tau_{yx}dxdzdy-\frac{\partial\tau_{yx}}{\partial y}dxdz\frac{dy^2}{2}=0
\end{align*}
両辺を\(dxdydz\)で割り、\(dx,dy\to0\)の極限をとると
$$\tau_{xy}+\frac{\partial\tau_{xy}}{\partial x}\frac{dx}{2}-\tau_{yx}-\frac{\partial\tau_{yx}}{\partial y}\frac{dy}{2}=0$$
$$\tau_{xy}=\tau_{yx}$$
を得る。
\(x\)面、\(y\)面についても同様にすれば
$$\tau_{yz}=\tau_{zy},\tau_{zx}=\tau_{xz}$$
となる。応力テンソルの対称性が示された。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]



