ここから、理想気体の力学について学んでいく。
まずは、理想気体で成り立つ基礎的な式をざっと確認しておく。
理想気体に関する基本事項
理想気体
とは、気体分子の大きさがゼロで、分子間力(ファンデルワールス力)が働かないと仮定した気体のことをいう。
理想気体は、絶対零度(0K)において体積がゼロになる。実際の気体(実在気体という)ではこのようなことは起こり得ない。
ボイル・シャルルの法則
圧力をp、密度をρ、気体定数をR、温度をTとする。
理想気体においては、温度一定のもとで圧力が体積に反比例する「ボイルの法則」と、圧力一定のもとで温度が体積に比例する「シャルルの法則」が成立する。
これらを合わせて、以下の式が成り立つ。
ただし、v=1/ρは比容積である。
熱力学第1法則
気体の内部エネルギーをeとする。
気体に与えられた熱量をdq、外部から加えられた仕事をdwとすると、内部エネルギーの変化deは
で与えられる。これはエネルギー保存の式である。
図のようなシリンダーの中の気体について考える。
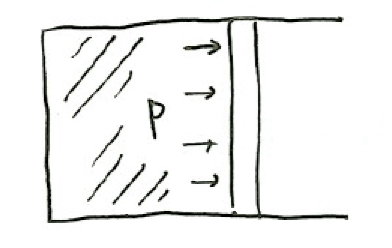
圧力pの気体が体積dvだけ膨張したとき、気体が外部にする仕事は
$$w_{out}=pdv$$
であるので、気体がされる仕事は-pdvで与えられる。よって、
$$de=dq-pdv$$
となる。
エンタルピーとエントロピー
エンタルピー
hは、次式で定義される。
エンタルピー変化は、圧力一定(dp=0)のとき
となる。すなわち、一定圧力で移動する熱はエンタルピー変化に等しい。
エントロピーSは、次式で定義される。
これをクラウジウスの式と呼ぶ。
状態の変化する方向はエントロピーの増大する方向であり、このことを熱力学第2法則という。
比熱
比熱
とは、単位質量の物体の温度を1K上げるために必要な熱量のことをいう。
$$C=\frac{dq}{dT}$$
定圧比熱と定積比熱
(1) 圧力一定での比熱を、定圧比熱という。
(2) 体積一定での比熱を、定積比熱という。
マイヤーの関係式(Mayer’s relation)
定圧比熱と定積比熱の間には、次の関係式が成立する。
\[
\begin{align*}
C_p&=\left(\frac{dh}{dT}\right) \\
& =\frac{d}{dT}(e+pv) \\
& =\frac{d}{dT}(e+RT) \\
& =\frac{de}{dT}+R=C_p+R
\end{align*}
\]
これを、マイヤーの関係式といい、気体分子によらず成立する。
比熱比
定圧比熱と定積比熱の比を、比熱比という。
比熱比を用いると、定圧・定積比熱は次のように書くことができる。
$$C_p=\gamma C_v=\gamma(C_p-R)$$
より、
$$C_p=\frac{\gamma R}{\gamma-1} ,C_v=\frac{R}{\gamma-1}$$
断熱過程
外部から熱の出入りがない場合(dq=0)を、断熱過程という。
このとき
$$dq=de+pdv=C_vdT+pdV=0$$
となる。ボイル・シャルルの法則よりpdv+vdp=RdT、上式よりdTを消去する。
$$pdv+vdp=R・\left(-\frac{pdv}{C_v}\right)$$
マイヤーの関係式も用いて整理すると
$$C_v・vdp+C_p・pdv=0$$
$$\gamma・\frac{dv}{v}+\frac{dp}{p}=0$$
よって、
となる。
また、同じく
$$Tv^{\gamma-1}=const ,Tp^{\frac{1-\gamma}{\gamma}}=const$$
も成立する。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]






