衝撃波
圧力などが不連続に急変する現象を衝撃といい、その断面を衝撃波と呼ぶ。
衝撃波は、波面と伝播方向によって垂直衝撃波・斜め衝撃波・離脱衝撃波に分類できる。
[mathjax] 垂直衝撃波については以下の記事を参照ください。 [sitecard subtitle=関連記事 url=https://ramenhuhu.com/fluid-shockwave] この記事では、発展形[…]
以下では、波面と伝播方向が垂直な垂直衝撃波について論じる。
垂直衝撃波
図のような管の中で衝撃波が発生しているとし、その両側の物理量の間に成立する関係式を導いていく。
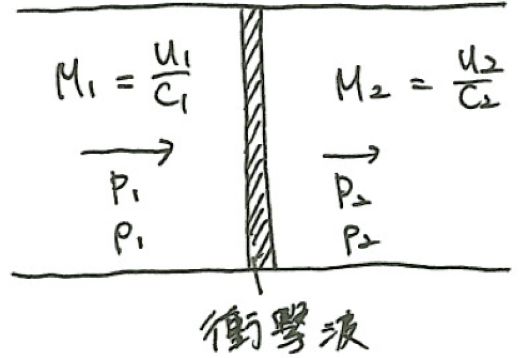
連続方程式より
$$\frac{\partial(\rho u)}{\partial x}=0 ・・・ \rho u=const$$
$$\rho_1u_1=\rho_2u_2 ・・・①$$
運動量方程式より
$$\rho_2u_2^2-\rho_1u_1^2=p_1-p_2 ・・・②$$
①、②および音速の式より
$$u_1-u_2=\frac{p_2}{\rho_2u_2}+\frac{p_1}{\rho_1u_1}=\frac{c_2^2}{\gamma u_2}+\frac{c_1^2}{\gamma u_1}$$
次に、エネルギー式
$$\frac{u_1^2}{2}+\frac{c_1^2}{\gamma-1}=\frac{u_2^2}{2}+\frac{c_2^2}{\gamma-1}=\frac{1}{2}\frac{\gamma+1}{\gamma-1}{c^*}^2$$
より、
$$\frac{c_2^2}{\gamma u_2}=\frac{\gamma+1}{2\gamma}\frac{{c^*}^2}{u_2}-\frac{\gamma-1}{2\gamma}u_2$$
$$\frac{c_1^2}{\gamma u_1}=\frac{\gamma+1}{2\gamma}\frac{{c^*}^2}{u_1}-\frac{\gamma-1}{2\gamma}u_1$$
したがって、
整理すると
$$\frac{\gamma+1}{2\gamma}・\frac{{c^*}^2}{u_1u_2}+\frac{\gamma-1}{2\gamma}=1$$
$$∴\frac{{c^*}^2}{u_1u_2}=\frac{c^*}{u_1}・\frac{c^*}{u_2}=\frac{1}{M_1^*・M_2^*}=1$$
を得る。
先に求めた、\(M\)と\(M^*\)の関係式
$$M^2=\frac{2}{\left(\frac{\gamma+1}{{M^*}^2}\right)-(\gamma-1)}$$
より、\(M\)と\(M^*\)の関係は
\[
\begin{cases}
M>1でM^*>1 \\
M<1でM^*<1
\end{cases}
\]
であることがわかる。したがって
$$M_2^*>1ならM_2>1であり、M_1^*・M_2^*=1からM_1^*<1なのでM_1<1$$
の2パターンが考えられる。
前者は超音速から亜音速への変化、後者は亜音速から超音速への変化を表す。
現実には、超音速⇒亜音速のパターンしか起こり得ない。これは、後の項でエントロピー変化に基づいて考察する。
密度比・圧力比・温度比
次に、密度比、圧力比、温度比を求める。
まず、\(M\)と\(M^*\)の関係を\(M^*=\cdots\)の形に書き換える。
さらに、マイヤーの関係式より
$$\frac{(\gamma+1)M_1^2}{2+(\gamma-1)M_1^2}・\frac{(\gamma+1)M_2^2}{2+(\gamma-1)M_2^2}=1$$
$$∴M_2^2=\frac{2+(\gamma-1)M_1^2}{2\gamma M_1^2-(\gamma-1)}$$
密度比および速度比は、連続方程式(①式)から
$$\frac{\rho_1}{\rho_2}=\frac{u_2}{u_1}=\frac{u_1u_2}{u_1^2}=\frac{{c^*}^2}{u_1^2}=\left(\frac{1}{M_1^*}\right)^2$$
圧力比は、運動量式(②式)から
$$p_2-p_1=\rho_1u_1^2-\rho_2u_2^2=\rho_1u_1(u_1-u_2)$$
\[
\begin{align*}
∴\frac{p_2-p_1}{p_1} &=\frac{\rho_1}{p_1}・u_1^2\left(1-\frac{u_2}{u_1}\right) \\
& =\gamma\frac{u_1^2}{c^2}・\left(1-\frac{2+(\gamma-1)M_1^2}{(\gamma+1)M_1^2}\right) \\
& =\frac{2\gamma}{\gamma+1}(M_1^2-1)
\end{align*}
\]
温度比は、音速の式から
$$\frac{T_2}{T_1}=\frac{c_2^2}{c_1^2}=\left(\frac{\rho_1}{\rho_2}\right)・\left(\frac{p_2}{p_1}\right)$$
密度比および圧力比の式を代入して整理すると
エントロピー変化
最後に、エントロピー変化\(S_2-S_1\)を考える。
エネルギー保存(熱力学第1法則)、比熱の定義式、ボイル・シャルルの法則より
$$dq=de+pdv=C_vdT+RT\frac{dv}{v}$$
である。よって、エントロピーの定義から
\[
\begin{align*}
S_2-S_1=\int\frac{dq}{T}&=\int\frac{C_v}{T}dT+\int R\frac{dv}{v} \\
& =C_v\ln\left(\frac{T_2}{T_1}\right)+R\ln\left(\frac{v_2}{v_1}\right)
\end{align*}
\]
ここで、
および定圧比熱と定積比熱のマイヤーの関係式、比熱比より
\begin{align*}
S_2-S_1&=C_v\left\{\ln\left(\frac{p_2}{p_1}\right)+\ln\left(\frac{v_2}{v_1}\right)\right\}+R\ln\left(\frac{v_2}{v_1}\right) \\
& =C_v\ln\left(\frac{p_2}{p_1}\right)+C_p\ln\left(\frac{v_2}{v_1}\right) \\
& =C_v\ln\left(\frac{p_2}{p_1}\right)-C_p\ln\left(\frac{\rho_2}{\rho_1}\right) \\
& =\frac{R}{\gamma-1}\ln\left(\frac{p_2}{p_1}\right)-\frac{\gamma R}{\gamma-1}\ln\left(\frac{\rho_2}{\rho_1}\right) \\
& =R\ln\left\{\left(\frac{p_2}{p_1}\right)^{\frac{1}{\gamma-1}}・\left(\frac{\rho_2}{\rho_1}\right)^{-\frac{\gamma}{\gamma-1}}\right\}
\end{align*}
\]
圧力比・密度比の式を代入して
を得る。
ここで、\(M_1^2-1=m\)とおくと
\(m\)が十分小さいとき、右辺の各項を級数展開して係数の和を求めると
$$\frac{S_2-S_1}{R}≒\frac{2}{3}\frac{\gamma}{(\gamma+1)^2}m^3$$
$$∴S_2-S_1=\frac{2}{3}\frac{\gamma R}{(\gamma+1)^2}(M_1^2-1)^3$$
熱力学第2法則(エントロピー増大)より、
$$S_2-S_1\ge0 ⇒ M_1>1 ⇒ M_2<1$$
となり、垂直衝撃波が生じるのは超音速から亜音速へ変化するときであることが確認できた。
また、圧力比の式を思い出すと
$$M_1^2-1=\frac{\gamma+1}{2\gamma}\frac{\Delta p}{p_1} (\Delta p=p_2-p_1)$$
より、
$$\frac{S_2-S_1}{R}=\frac{\gamma+1}{12\gamma^2}\left(\frac{\Delta p}{p_1}\right)^3$$
となる。\(\Delta p\)が小さいとき、等エントロピー流とみなすことができる。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]





