はさみうちの原理を利用した極限値の計算の有名な例である、
の求め方を解説していきます。
まず、下図のような状態を考えます。
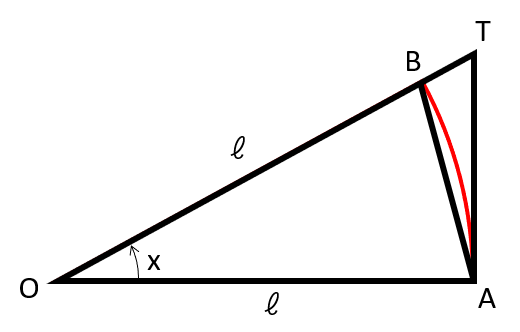
∠OAT\(=\pi/2\)、∠AOT\(=x\) \((0\lt x\lt \pi/2)\)とし、OAを半径とする円とOTとの交点をBとします。
ここで、三角形OAT、扇形OAB、三角形OABの面積の大小関係について考えます。
\(~~~~~△OAT=(底辺)×(高さ)/2=OA×AT/2=l×l\tan x/2\)
\(~~~~~扇形OAB=(半径)×(弧長)/2=l×lx/2\)
\(~~~~~△OAB=l×l\sin x/2\)
なので、その大小関係から次の不等式が成り立ちます。
$$\frac{l^2}{2}\sin x<\frac{l^2}{2} x<\frac{l^2}{2}\tan x$$
$$1<\frac{x}{\sin x}<\frac{1}{\cos x}$$
$$\cos x<\frac{\sin x}{x}<1$$
\(\cos x\)も\(\sin x/x\)も偶関数なので、\(x\to+0\)でも\(x\to-0\)でも同じです。つまり、上式は\(0\lt|x|\lt\pi/2\)で成立します。
さて、\(x\to 0\)のとき\(\cos x\to1\)なので、はさみうちの原理を適用することができます。(はさみうちの原理についてはこちらの記事)
不等号の両側が1に収束するということは、真ん中も1に収束する、ということですね。
したがって、
$$\lim_{x \to 0}\frac{\sin x}{x}=1$$
となります。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




