今回から、積分法に入っていきます。
まずは不定積分を定義し、積分の計算になれるところから始めたいと思います。
不定積分とは
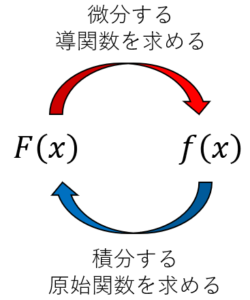
微分・積分を図に示すと上ような関係になっています。微分と積分は逆の演算をすることになります。
ただし、実際に微分と積分が本当に逆演算になっているかどうかは証明しなくてはいけません。この事実を微積分学の基本定理と呼び、後ほど証明します。
積分定数
\(F(x)、G(x)\)がともに\(f(x)\)の原始関数であるとすると
これより、次が成り立ちます。
\(F(x)\)を\(f(x)\)の区間\(I\)における一つの原始関数とすると、\(f(x)\)の\(I\)におけるすべての原始関数は
$$F(x)+C (C:定数)$$
の形に表すことができる。
この定数Cのことを、積分定数(integral constant)と呼びます。
ある原始関数が見つかったとすると、それに定数を加えたものはすべて原始関数である、ということです。
\(f(x)\)の原始関数を
$$\int f(x)dx$$
で表し、これを\(f(x)\)の不定積分と呼ぶ。
\(F(x)=\int f(x)dx\)と\(F'(x)=f(x)\)は同じ事を意味しています。
不定積分の計算
定数倍・加減
定数倍や関数の足し算引き算については、くくりだすことができます。
部分積分法
$$\int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx$$
少しややこしい形をしていますが、よく使う公式です。(例えば\(\log x\)の積分)
\(g(x)=\int g'(x)dx\)なので、\(g'(x)\)を改めて\(g(x)\)と置くことで
と書くこともできます。関数の積の積分公式とも言えますね。
置換積分法
\(x=\phi (t)\)とおくとき、\(\phi\)が\(C^1\)級ならば
$$\int f(x)dx=\int f(\phi (t))\phi^{\prime}(t)dt$$
積分変数を変換する公式です。合成関数の積分などで使われます。
基本的な関数の不定積分
ここでは、積分定数は省略します。
$$\int x^\alpha dx=\frac{1}{\alpha +1}x^{\alpha +1} (\alpha \not =-1)$$
$$\int \frac{dx}{x}=\log |x|$$
$$\int e^x dx=e^x、\int a^x dx=\frac{a^x}{\log a}$$
$$\int \log |x|dx=x\log |x|-x$$
$$\int \sin (ax+b)dx=-\frac{1}{a}\cos (ax+b)$$
$$\int \cos (ax+b)dx=\frac{1}{a}\sin (ax+b)$$
いずれも基本的な式です。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





