はりに荷重が作用すると、はりの内部には応力が発生する。
はりの力のつり合いを考えることで、はりの任意の断面に生じるせん断力および曲げモーメントについて考えよう。
せん断力と曲げモーメント
に荷重が作用している場合を考えよう。
支点には反力が生じ、外力および曲げモーメントの和が0となることではりはつり合いを保つ。
はりに集中荷重\(W_1,W_2\)が作用し、支点\(A,B\)に反力\(R_A,R_B\)が生じているとする。
下図のように、はりを断面\(X\)で切断して左右2つの部分に分けて考える。
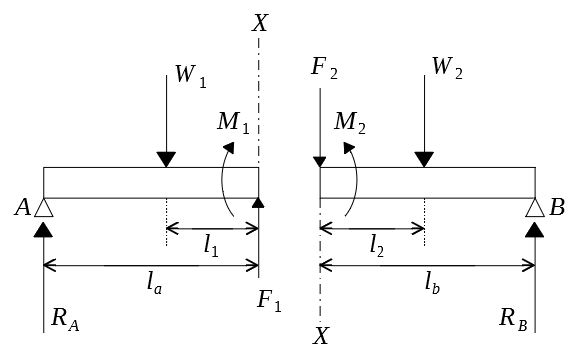
左側の部分が平衡を保つためには、切断面に沿って何らかの力の作用が必要であり、同時に曲げモーメントが生じなければならない。
これらの力を\(F_1\)および\(M_1\)とすると、つり合い条件は
\begin{align*}
W_1-R_A-F_1=0 \\
W_1l_1-R_Al_a-M_1=0
\end{align*}
これより、\(F_1\)および\(M_1\)は
\begin{cases}
F_1=R_A-W_1 \\
M_1=W_1l_1-R_Al_a
\end{cases}
となる。
右側の部分についても同様にして、切断面に図の方向に\(F_2\)および\(M_2\)が作用するとすると
\begin{cases}
F_2=R_B-W_2 \\
M_2=W_2l_2-R_Bl_b
\end{cases}
を得る。
ここで、はりに作用する外力のつり合いと、断面X上の点に関するモーメントのつり合いを考えると
\begin{align*}
W_1-R_A&=R_B-W_2 \\
W_1l_1-R_Al_a&=W_2l_2-R_Bl_b
\end{align*}
である。これらと、先に求めた\(F,M\)の式を比較すると
\begin{align*}
F_1&=F_2 \\
M_1&=M_2
\end{align*}
なる関係が得られる。すなわち、\(F_1\)と\(F_2\)および\(M_1\)と\(M_2\)はそれぞれ「大きさが等しく」、「方向が逆」であることがわがる。
\(F_1\)、\(F_2\)をはりの断面に作用するせん断力、\(M_1\)、\(M_2\)を曲げモーメントという。
断面内の応力分布
上で見たように、荷重が作用しているはりの任意の断面にはせん断力および曲げモーメントが作用している。
これらに抵抗するため、\(X\)断面には断面に平行に作用するせん断応力と、断面に垂直に作用する垂直応力とが生じなくてはならない。
しかし、真直はりでは垂直応力の作用方向に外力が作用しないので、垂直応力の合計はゼロになる。このため、断面の一部には引張応力が、残りの部分には圧縮応力が存在する。
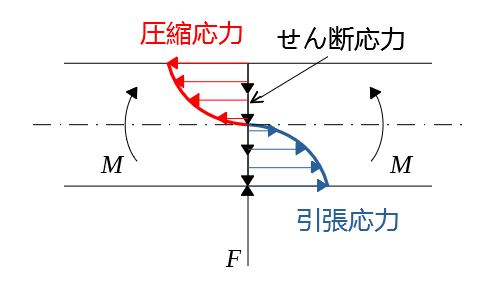
例えば、上でみたはりにおいては図のような応力分布をとる。
垂直応力については、中心軸の上側では圧縮応力、下側では引張応力が生じ、中心軸上で0になる。一方、せん断応力は存在する。
例題
はりに作用する力について、簡単な計算問題を解いてみよう。
1.図のように、2つの集中荷重がかかっているはりの反力を求めよ。
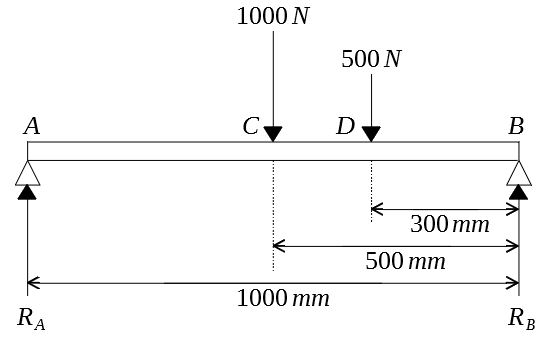
(解)
B点まわりのモーメントのつり合いより
$$R_A=\frac{W_1l_1+W_2l_2}{l}=\frac{1000・500+500・300}{1000}=650(N)$$
また、はりに作用する外力のつり合いより
$$R_B=W_1+W_2-R_A=1000+500-650=850(N)$$
(解答終)
(ポイント)
片持ちはりでは、支点の反力は固定端に生じ、大きさは荷重と等しく向きが逆である。
(解)
支点反力ははりの固定端に生じ、その大きさは
$$R=500(N)$$
である。
自由端からの距離が\(x\)である断面の固定端側を考えると、外力は反力のみなので
$$F_x=R=500(N)$$
\(x\)を次第に大きくして、固定端に達してもせん断力は一定である。よって任意の断面に生じるせん断力は
$$F=500(N)$$
である。
また、自由端から0.2mの断面における曲げモーメントは
$$M_{0.2}=500・0.2=100(Nm)$$
である。
(解答終)





