前回は空間中の曲線について曲率を定義していきました。
しかし、通常曲率を求める対象は空間曲線ではなく、平面上の曲線すなわち\(y=f(x)\)の関数であることが多いと思います。
今回は平面上の関数について曲率を求める式を導出し、具体的な計算例を示していきます。
平面上の曲線と曲率
まず空間曲線を平面に落とし込みます。
平面曲線
平面曲線は空間曲線\(\mathbf{r}=(x(t), y(t), z(t))\)において、\(z(t)=0\)の場合と考えることができます。
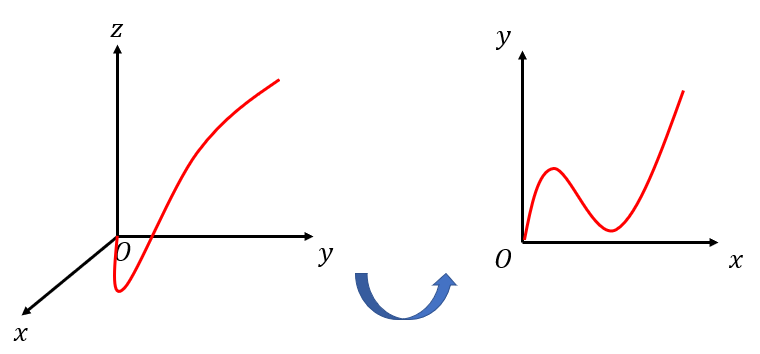
曲線を\(xy\)-平面に投影してできる線ですね。
簡単のため、\(z\)座標を省略し
$$曲線C:\mathbf{r}=(x(t), y(t))$$
を正則な\(C^2\)級曲線とします。
平面曲線の曲率
\(C\)上の点\(P(t)\)における接線が\(x\)軸となす角を\(\theta\)とするとき、\(\displaystyle\kappa =\frac{d\theta}{ds}\)を曲率とする。
$$\kappa=\frac{\dot{\theta}}{v}=\frac{\dot{x}\ddot{y}-\ddot{x}\dot{y}}{v^3}=\frac{\dot{x}\ddot{y}-\ddot{x}\dot{y}}{(\dot{x}^2+\dot{y}^2)^\frac{3}{2}}$$
特に、曲線\(y=f(x)\)については、\(x=t, y=f(t)\)と考えて
$$\kappa=\frac{f^{\prime\prime}(x)}{\left( 1+f'(x)^2 \right)^\frac{3}{2}}$$
曲率の計算例
具体的な曲線に対して曲率を計算してみましょう。
(1) 円の曲率
曲率は曲線を円で近似したものなので計算するまでもないのですが、試しに計算してみましょう。
円の媒介変数表示は、\((x, y)=(a\cos\theta, a\sin\theta) (0\le \theta \le 2\pi)\)で与えられます。
これを曲率の公式に代入すると、
\[
\begin{align*}
\kappa&=\frac{\dot{x}\ddot{y}-\ddot{x}\dot{y}}{(\dot{x}^2+\dot{y}^2)^\frac{3}{2}} \\
&=\frac{-a\sin \theta・(-a\sin \theta)-(-a\cos \theta)・a\cos \theta}{\left( (-a\sin \theta)^2+(a\cos \theta)^2 \right)^\frac{3}{2}} \\
&=\frac{a^2}{a^3} \\
&=\frac{1}{a}
\end{align*}
\]
となります。当然の結果ですが、円の曲率は一定で半径の逆数に、曲率半径は円の半径に一致します。
(2) 楕円の曲率
円の発展形として、楕円について考えます。
$$楕円の方程式:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 (a>0, b>0)$$
媒介変数表示すると、\((x, y)=(a\cos \theta, b\sin \theta) (0\le \theta \le 2\pi)\)なので
\[
\begin{align*}
\dot{x}\ddot{y}-\ddot{x}\dot{y}&=(-a\sin\theta)・(-b\sin\theta)-(-a\cos\theta)・(b\cos\theta) \\
&=ab(\sin^2\theta+\cos^2\theta) \\
&=ab
\end{align*}
\]
$$\dot{x}^2+\dot{y}^2=a^2\sin^2\theta+b^2\cos^2\theta$$
よって、
$$\kappa=\frac{ab}{(a^2\sin^2\theta+b^2\cos^2\theta)^\frac{3}{2}}$$
さて、楕円の曲率の式が求まりました。これについて少し考察をしてみましょう。
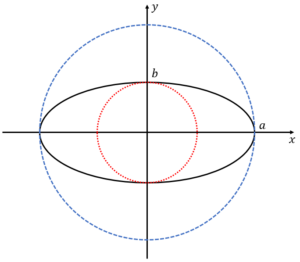
\(a\gt b\gt0\)とします。\(a\)を長軸半径、\(b\)を短軸半径とよびます。
このとき、分母の中身について
$$a^2\sin^2\theta+b^2\cos^2\theta=(a^2-b^2)\sin^2\theta+b^2$$
$$a^2-b^2>0 かつ 0\le \sin^2\theta \le1$$
なので、
$$b^2\le a^2\sin^2\theta+b^2\cos^2\theta \le a^2$$
したがって、楕円の曲率の最大値・最小値は
$$\kappa_{max}=\frac{ab}{(b^2)^\frac{3}{2}}=\frac{a}{b^2} (\theta=0,\piのとき)$$
$$\kappa_{min}=\frac{ab}{(a^2)^\frac{3}{2}}=\frac{b}{a^2} \left(\theta=\frac{\pi}{2},\frac{3\pi}{2}のとき\right)$$
となります。(上図参照)
曲率円と曲率の中心
\(C\)上の点\(P\)において、接線に接し\(\displaystyle\rho=\frac{1}{|\kappa|}\)を半径とする円のうち
\(C\)と同じ側にある円を\(P\)における曲率円、その中心を曲率の中心と呼ぶ。
曲率中心の計算
\(y=f(x)\)について、点\((x, f(x))\)における曲率中心\((\xi,\eta)\)を求めよう。
接線ベクトル\((1,y’)\)を\(+90^\circ\)だけ回転した\((-y’,1)\)から
$$(\xi,\eta)=(x,y)+\frac{\rho(-y’,1)}{\sqrt{1+y’^2}}$$
\[
\begin{cases}
\displaystyle\xi=x-\frac{\rho y’}{\sqrt{1+y’^2}}=x-\frac{y'(1+y’^2)}{y”} \\
\displaystyle\eta=y+\frac{\rho}{\sqrt{1+y’^2}}=y+\frac{1+y’^2}{y”}
\end{cases}
\]
縮閉線と伸開線
平面曲線\(C\)の曲率中心の軌跡\(E\)を\(C\)の縮閉線といい、これに対して\(C\)を\(E\)の伸開線という。
これについては別の機会があれば書いていきたいと思います。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





