曲率と曲率半径の求め方

微分積分学

前回は空間曲線をベクトルによって表記することを学びました。

この記事では、曲線の特徴量である曲率と曲率半径について学習していきます。

1 曲率とはなにか
2 曲率・曲率半径の定義
3 接触平面
- 3.1 単位主法線ベクトル
- 3.2 接触平面

曲率とはなにか

日常生活ではあまり聞きなれない言葉かもしれませんが、私たちの生活の中で曲率(または曲率半径)は多く活用されています。

たとえば、道路のカーブやジェットコースターのループなどは曲率の知識を活かして設計がなされています。もしそうでなければ、急ハンドルでないと曲がり切れない道や体に負担のかかる乗り物が世の中にあふれてしまいます。

曲率(curvature)とは、曲線(あるいは曲面)上のある点での曲がり具合を表す量です。簡単に図解すると、次のようになります。

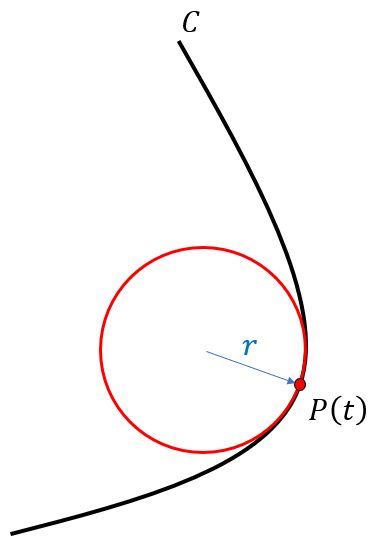
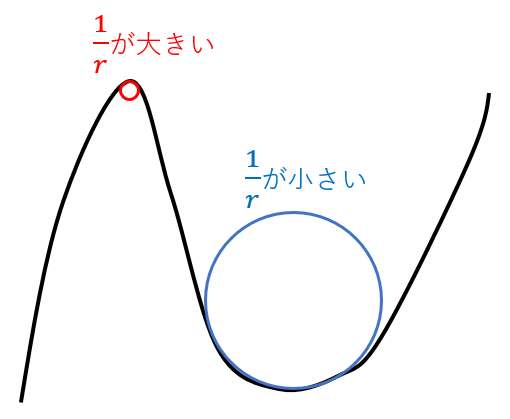
曲線$C$上の点$P(t)$における曲率とは、その点での曲がり具合を円で近似したときの半径$r$の逆数として与えられます。この円の半径(曲率半径という)が小さいということは、曲率が大きいことを表します。上の図から、曲率が大きい場合は曲がり具合がより急であることが分かります。

曲率・曲率半径の定義

それでは、一般の曲線に対して曲率を定義していきます。

曲線$C$の始点から点$P(t)$までの弧長を$s=s(t)$とすると、

$$\frac{ds}{dt}=|\dot{\mathbf{r}}|=v$$

である。したがって、$s$は$t$の狭義増加な$C^1$級関数となり、逆関数の微分公式より$t$も$s$の$C^1$級関数となる。

$s$に関する微分を、以後「$\prime$」を用いて示すことにします。

$$\frac{d\mathbf{r}}{ds}=\frac{d\mathbf{r}}{dt}\frac{dt}{ds}=\frac{\frac{d\mathbf{r}}{dt}}{\frac{ds}{dt}}=\frac{\dot{\mathbf{r}}}{|\dot{\mathbf{r}}|}=\mathbf{t}$$

tは単位接線ベクトルでした。

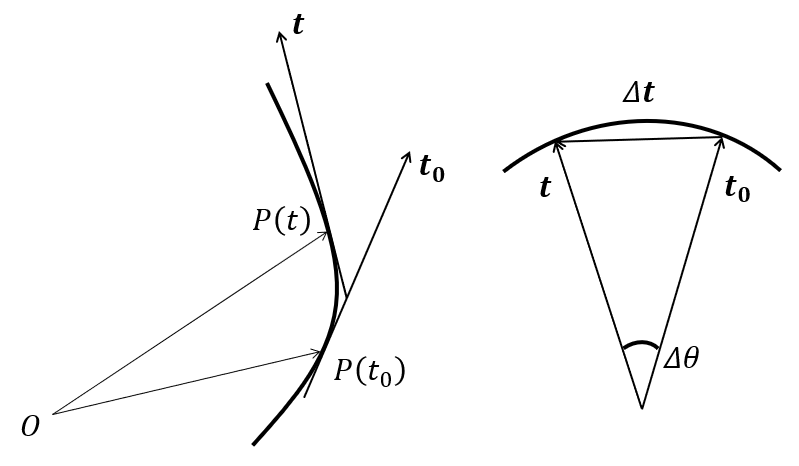
$t=t_0$における単位接線ベクトルを$\mathbf{t}_0$、$\mathbf{t}$と$\mathbf{t}_0$のなす角を$\Delta \theta$とする。$\Delta\mathbf{t}=\mathbf{t}-\mathbf{t}_0$、$\Delta s=s(t)-s(t_0)$として

\[
\begin{align*}
\lim_{\Delta\mathbf{t}\to 0}\frac{\Delta \theta}{|\Delta s|}&=\lim_{\Delta\mathbf{t}\to 0}\frac{\Delta \theta}{|\Delta \mathbf{t}|}\frac{|\Delta \mathbf{t}|}{|\Delta s|} \\
&=\lim_{\Delta\mathbf{t}\to 0} |\frac{\Delta\mathbf{t}}{\Delta s}| \\
&=|\frac{d\mathbf{t}}{ds}|=|\mathbf{t}’|
\end{align*}
\]

この値を、$C$の$t=t_0$における曲率と呼び、$\kappa$で表します。

$$\kappa =\lim_{\Delta\mathbf{t}\to 0}\frac{\Delta \theta}{|\Delta s|}=|\mathbf{t}’|=|\mathbf{r}^{\prime\prime}|$$

また、$\rho=1/\kappa$を曲率半径といいます。