偏微分を取り扱うために、平面上の点の集合について学んでおく必要があります。
ここでは、点集合と点列について考えていきます。
点集合
距離
平面上の2点\(P(x, y)、Q(x’, y’)\)の距離を\(d(P, Q)\)とかくことにします。すなわち
$$d(P,Q)=\sqrt{(x-x’)^2+(y-y’)^2}$$
距離は、次の性質をもちます。
(1)正値性
$$d(P,Q)\ge0 等号成立はP=Qのとき$$
(2)対称性
$$d(Q,P)=d(P,Q)$$
(3)三角不等式
$$d(P,R)\le d(P,Q)+d(Q,R)$$
点集合の定義
以下では、\(E\)は平面上の点からなる一つの集合(これを点集合といいます)を表すものとします。
点\(P\)とある正数\(\varepsilon\)に対して、集合
$$\{ Q|d(P,Q)<\varepsilon \}$$
を点\(P\)のε近傍とよびます。ε近傍は中心\(P\)、半径εの円の内部の点全体からなる集合です。
点\(P\)のある近傍が\(E\)に含まれるとき、\(P\)は\(E\)の内点であるといいます。
これに対して、\(P\)のある近傍で\(E\)と共有点を持たないものが取れるとき、\(P\)は\(E\)の外点であるといいます。
\(E\)の内点でも外点でもない点を\(E\)の境界点といいます。\(P\)が\(E\)の境界点であるための条件は、\(P\)のすべての近傍が\(E\)内の点も\(E\)に属さない点も含むことです。
図にすると次のようになります。
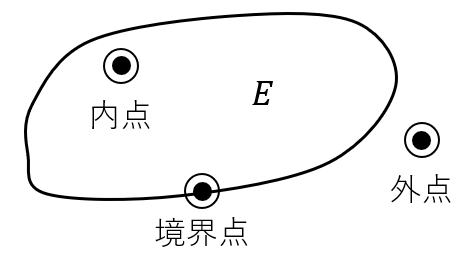
閉集合と開集合
の内点は\(E\)に属し、\(E\)の外点は\(E\)に属しません。\(E\)の境界点は\(E\)に属する場合も属さない場合もあります。
特に、\(E\)の境界点がすべて\(E\)に属すとき\(E\)は閉集合であるといい、反対に、\(E\)の境界点がどれも\(E\)に属さないときEは開集合であるといいます。
\(E\)の境界点全体からなる集合を\(E\)の境界とよび、\(\partial E\)とかきます。
集積点と孤立点
点\(P\)の任意の近傍が\(E\)の点を無限個含むとき、\(P\)を\(E\)の集積点といいます。
これは、\(P\)の任意の近傍が\(P\)と異なる\(E\)の点を少なくとも一つ含むことと同義です。\(E\)の内点はすべて\(E\)の集積点になります。
\(E\)の境界点で、\(E\)の集積点ではない点は明らかに\(E\)に属します。このような点を\(E\)の孤立点とよびます。
点列
平面上の(無限)点列\(\{P_n\}\)に対し定点\(P\)があり、\(d(P_n, P)\to0 (n\to\infty)\)が成り立つとき、\(\{P_n\}\)は\(P\)に収束するといい、\(P\)をその極限点と呼びます。
不等式
より\(P_n(x_n, y_n)、P(x, y)\)とすれば、\(P_n\to P\)となることは\(x_n\to x、y_n\to y\)となることを意味します。
これより、次のことがいえます。
1)点列の極限点は存在するならばただ一つである。
2)収束する点列\(\{P_n\}\)は有界である。すなわち、点集合\(\{P_n|n\in\mathbb{N}\}\)はある円板に含まれる。
3)収束する点列の任意の部分点列は同じ極限点に収束する。
コーシーの判定条件
点列\(\{P_n\}\)が収束するための条件は
$$d(P_m,P_n)\to0 (m,n\to\infty)$$
となることである。すなわち、任意の正数\(\varepsilon\)に対してある\(N\)をとれば
$$d(P_m,P_n)<\varepsilon (m,n>N)$$
を満たすようにできることである。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




