ここでは、定積分を用いた実用的な計算について考えていきます。
正項級数の積分判定法
定理
$$f(x)は[1,\infty)上で正値かつ単調減少とする。このとき、$$
$$正項級数\sum_{n=1}^{\infty}f(n)と広義積分\int_1^{\infty}f(x)dxは同時に収束・発散する$$
$$\sum_{n=1}^{\infty}\frac{1}{n^p}の収束・発散について考えます。$$
(ⅰ)p≦0のとき、明らかに発散する
(ⅱ)p>0のとき
$$f(x)=\frac{1}{x^p}(x\ge1)として上の定理を適用する$$
$$\sum_{n=1}^{\infty}\frac{1}{n^p}はp>1のとき収束し、p\le1のとき発散する$$
面積
直交座標系
y=f(x)を[a,b]上の連続関数とし、f(x)≧0とします。x軸と直線x=a, x=bおよび曲線y=f(x)で囲まれた図形をDとします。
$$D=\{ (x,y)|a\le x\le b, 0\le y\le f(x) \}$$
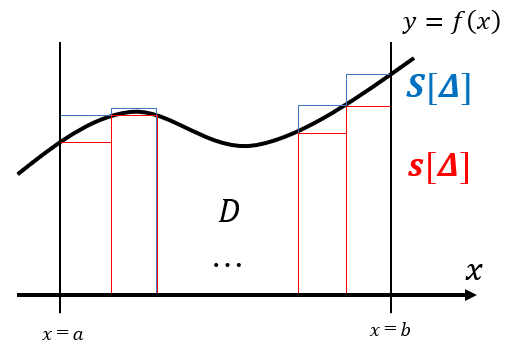
Dの面積をAとすると、s[Δ]≦A≦S[Δ]が成り立ちます。|Δ|→0として
$$A=\int_a^b f(x)dx$$
定積分により面積を求めることができます。
極座標系
曲線が極方程式r=f(θ) (α≦θ≦β)で表されているとき、この曲線と動径θ=α、θ=βで囲まれた部分の面積Aを求めます。
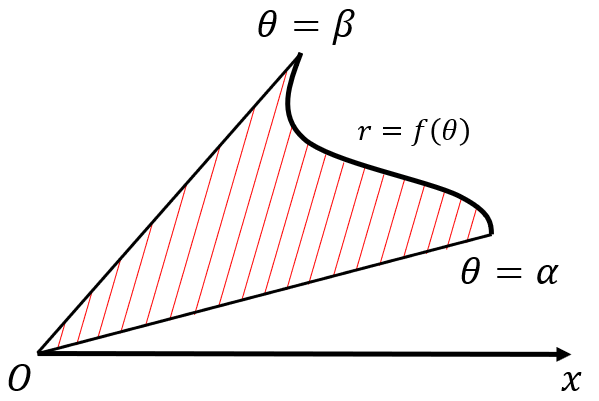
まず、扇形の面積の公式を思い出しましょう。半径ρ、中心角ωの扇形の面積は、
$$\frac{1}{2}\rho^2\omega$$
で与えられます。このことから、[α, β]の分割Δに対して
$$\frac{1}{2}s[\Delta,f^2]\le A\le \frac{1}{2}S[\Delta,f^2]$$
|Δ|→0のとき、不等式の両端はともに
$$\frac{1}{2}\int_{\alpha}^{\beta}f^2(\theta)d\theta$$
に収束します。したがって、
$$A=\frac{1}{2}\int_{\alpha}^{\beta}r^2d\theta\left(=\frac{1}{2}\int_{\alpha}^{\beta}f^2(\theta)d\theta\right)$$
曲線の長さ
平面上で2点A, Bを結ぶ曲線
$$C:\mathbb{r}=\mathbb{r}(t) (\alpha\le t\le\beta)$$
を考えます。
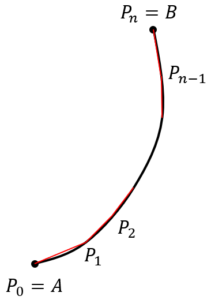
区間[α, β]の分割
$$\Delta:\alpha=t_0<t_1<…<t_n=\beta$$
に対して、tiに対応するC上の分点をPiとするとき、これらの分点P0=A, P1, …, Pn=Bを結んで得られる折れ線の長さを
$$L_{\Delta}=\sum_{i=1}^n \overline{P_{i-1}P_i}$$
とかきます。[α, β]のすべての分割Δに関する上限
$$\sup L_{\Delta}=L$$
をCの長さまたは弧長といいます。L<∞のとき、Cは長さを持つといいます。
$$C^1級の曲線\mathbb{r}=\mathbb{r}(t)=(x(t),y(t))(\alpha\le t\le\beta)の長さLは次式で与えられる$$
$$L=\int_{\alpha}^{\beta} |\mathbb{r}'(t)|dt=\int_{\alpha}^{\beta} \sqrt{x’^2(t)+y’^2(t)}dt$$






