広義積分の計算
の応用で、広義積分を計算することができる。
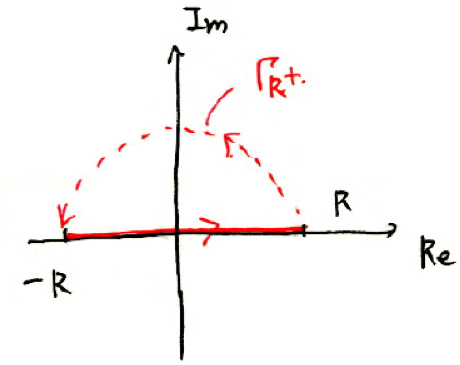
上のように、-RからRまでの直線経路と、原点を中心とする半径Rの半円経路を考える。こうしてできる閉曲線経路をとることで
$$\int_{-\infty}^{\infty} \to \lim_{R\to\infty}\int_{-R}^R+\lim_{R\to\infty}\int_{\Gamma_{R^+}}$$
のように積分を分解することができる。
このとき、右辺第二項の積分が0に収束するならば、留数定理を用いて広義積分を求めることが可能である。例題で確認しよう。
被積分関数の分子にあたる部分が正の場合は上側の半円、負の場合は下側の半円からなる経路を用いる。
反時計回りを正とするため、負の場合は時計回りなので”-”がつくことに注意する。
例題
$$f(z)=\frac{e^{-iz}}{(z^2+1)(z+2i)^2}とおく。$$
まず、f(z)の分子について
\[
\begin{align*}
|e^{-iz}| &=|e^{-i(x+iy)}|=|e^{y-ix}| \\
& =|e^y||e^{-ix}|=|e^y||\cos x+i\sin x| \\
& =|e^y|\to 0 (y\to -\infty)
\end{align*}
\]
このとき、下図のような経路でのf(z)の積分値は、y=Im zが負の無限大に近づくときにf(z)が0に近づくことから、下側の半円経路での積分も0になる。
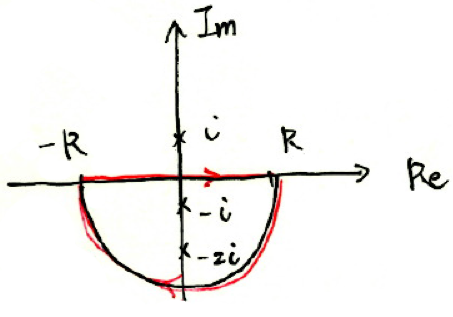
よって、
$$I=\lim_{R\to\infty}\int_{-R}^{R}f(z)dz+\lim_{R\to\infty}\int_{\Gamma_{R^-}}dz$$
において、留数定理により
$$I=-2\pi i\left(\mathrm{Res}_{z=-i}f(z)+\mathrm{Res}_{z=-2i}f(z)\right)$$
となる。(マイナスがつくことに注意!)
さて、
$$\mathrm{Res}_{z=-i}f(z)=\lim_{z\to -i}\frac{e^{-iz}}{(z-i)(z+2i)^2}=\frac{1}{2ie}$$
であるので、これを代入して
$$I=-\pi i\left(\frac{1}{2ie}+\frac{7i}{9e^2}\right)=-\frac{\pi}{e}+\frac{14\pi}{9e^2}$$






