連続方程式
流体力学で最も基本的な方程式の一つです。導出方法を理解しておきましょう。
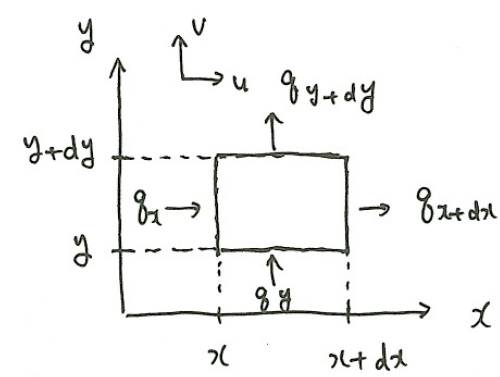
\(xy\)-座標系のなかに、辺の長さが\(dx、dy\)の領域を考える。
単位時間にこの領域に流れ込む流量を\(q_x、q_y\)とし、流れ出る流量を\(q_{x+dx}、q_{y+dy}\)とする。
領域内の流量の変化が密度の変化に等しくなるので、\(x\)方向の流速を\(u\)、\(y\)方向の流速を\(v\)とすれば、
$$q_x+q_y-(q_{x+dx}+q_{y+dy})=\frac{\partial\rho}{\partial t}dxdy$$
これを整理すると、
$$\frac{\partial\rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}=0$$
また、非圧縮性流体(\(\rho\)=一定)と仮定すると
$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$
を得る。
圧縮性流体の連続方程式
$$\frac{\partial\rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}=0$$
非圧縮性流体の連続方程式
$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$
例題:管の断面積が一定でない場合
断面積が一定でない管を流れる、一次元定常流に対する連続方程式を求めよ。
(解)
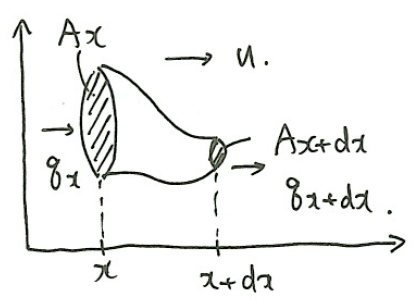
\(x\)における断面積を\(A(x)\)とおく。\(x\)から流入する流量を\(q_x\)、\(x+dx\)から流出する流量を\(q_{x+dx}\)、流速を\(u\)とすれば、(流量変化)=(質量変化)なので
$$q_x-q_{x+dx}=\frac{\partial(\rho Adx)}{\partial t}$$
$$\rho uA-\left(\rho uA+\frac{\partial(\rho uA)}{\partial x}dx\right)=\frac{\partial(\rho A)}{\partial t}dx$$
整理して、
$$\frac{\partial(\rho uA)}{\partial x}+\frac{\partial(\rho A)}{\partial t}=0$$
定常流(時間微分項が0)の場合
$$\frac{\partial(\rho uA)}{\partial x}=0$$
となる。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]






