新米夫婦のふたりごと

当ブログは記事内にプロモーションを含みます。ご了承ください。

貯気槽からの断熱流出モデル：ラバールノズルと物理量

流体力学 流体力学問題
十分に大きな貯気槽から断熱状態で気体が流出するとき、槽内と出口の音速比、温度比、密度比、圧力比を求めよ。

 

(解)

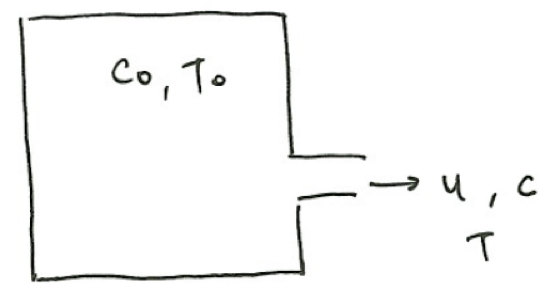
貯気槽では\(u=0\)と考えることができる。

エネルギー式より、

$$\frac{1}{2}u^2+\frac{c^2}{\gamma-1}=\frac{c_0^2}{\gamma-1}$$

この両辺を\(c^2\)で割ると

$$\frac{1}{2}\frac{u^2}{c^2}+\frac{1}{\gamma-1}=\frac{1}{\gamma-1}\frac{c_0^2}{c^2}$$

音速およびマッハ数の式から

$$\left(\frac{c_0}{c}\right)^2=\frac{T_0}{T}=1+\frac{\gamma-1}{2}M^2$$

 

次に、密度比と圧力比を求める。

ボイル・シャルルの式および断熱の式を用いると

$$\frac{T_0}{T}=\frac{\frac{p_0/\rho_0}{R}}{\frac{p/\rho}{R}}=\frac{p_0}{p}\frac{\rho}{\rho_0}=\left(\frac{\rho_0}{\rho}\right)^{\gamma-1}=\left(\frac{p_0}{p}\right)^{\frac{\gamma-1}{\gamma}}$$

と変形できる。したがって、

$$\frac{\rho_0}{\rho}=\left(\frac{T_0}{T}\right)^{\frac{1}{\gamma-1}}=\left(1+\frac{\gamma-1}{2}M^2\right)^{\frac{1}{\gamma-1}}$$

$$\frac{p_0}{p}=\left(\frac{T_0}{T}\right)^{\frac{\gamma}{\gamma-1}}=\left(1+\frac{\gamma-1}{2}M^2\right)^{\frac{\gamma}{\gamma-1}}$$

 

出口がラバールノズルになっているとき、スロート部(M=1)での各比も計算せよ。
(解)
スロートにおける音速を\(c^*\)とすると、エネルギー式より
$$\frac{c_0^2}{\gamma-1}=\frac{{c^*}^2}{2}+\frac{{c^*}^2}{\gamma-1}=\frac{1}{2}\frac{\gamma+1}{\gamma-1}{c^*}^2$$
よって、
$$\left(\frac{c_0}{c^*}\right)^2=\frac{T_0}{T^*}=\frac{\gamma+1}{2}$$
となる。また先ほどと同様にして

$$\frac{\rho_0}{\rho^*}=\left(1+\frac{\gamma-1}{2}\right)^{\frac{1}{\gamma-1}}=\left(\frac{\gamma+1}{2}\right)^{\frac{1}{\gamma-1}}$$

$$\frac{p_0}{p^*}=\left(1+\frac{\gamma-1}{2}\right)^{\frac{\gamma}{\gamma-1}}=\left(\frac{\gamma+1}{2}\right)^{\frac{\gamma}{\gamma-1}}$$

を得る。
まとめページ
流体力学

流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]

流体力学
流体力学問題
最新情報をチェックしよう！

流体力学の最新記事8件