運動量方程式の導出

流体力学

1 運動量方程式

運動量方程式

「衝撃波」を論じるための準備として、運動量保存の式を導出する。

一次元で考える。オイラーの運動方程式において、v=0、体積力=0として

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=-\frac{1}{\rho}\frac{\partial p}{\partial x}　・・・①$$

また、連続方程式より

$$\frac{\partial(\rho A)}{\partial t}+\frac{\partial(\rho uA)}{\partial x}=0　・・・②$$

$$①×A\rho　：　A\rho・\frac{\partial u}{\partial t}+A\rho u・\frac{\partial u}{\partial x}=-A・\frac{\partial p}{\partial x}$$$$②×u　：　u・\frac{\partial(\rho A)}{\partial t}+u・\frac{\partial(\rho uA)}{\partial x}=0$$

辺々足し合わせると

$$\left\{ A\rho・\frac{\partial u}{\partial t}+u・\frac{\partial(\rho A)}{\partial t}\right\}+\left\{ A\rho u・\frac{\partial u}{\partial x}+u・\frac{\partial(\rho uA)}{\partial x}\right\}=-A・\frac{\partial p}{\partial x}$$

ここで、積の微分公式より

$$A\rho・\frac{\partial u}{\partial t}+u・\frac{\partial(\rho A)}{\partial t}=\frac{\partial(A\rho u)}{\partial t}$$

$$A\rho u・\frac{\partial u}{\partial x}+u・\frac{\partial(\rho uA)}{\partial x}=\frac{\partial (A\rho u^2)}{\partial x}$$

$$-A・\frac{\partial p}{\partial x}=\frac{\partial A}{\partial x}p-\frac{\partial (Ap)}{\partial x}$$

である。これらから

$$\frac{\partial(A\rho u)}{\partial t}+\frac{\partial (A\rho u^2)}{\partial x}=\frac{\partial A}{\partial x}p-\frac{\partial (Ap)}{\partial x}$$

となる。

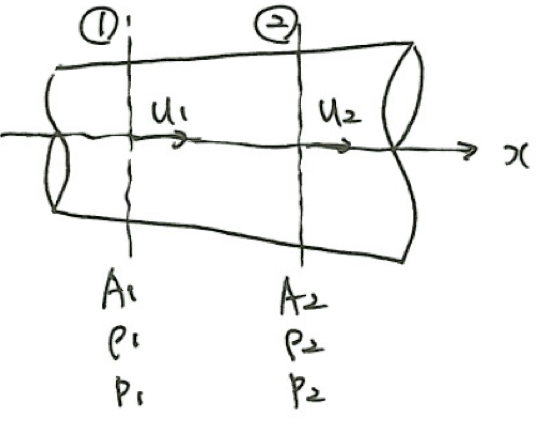
図のような検査面をとり、xについて積分する。

\[
\begin{align*}
\frac{\partial}{\partial t}&=\int_{①}^{②}(A\rho u)dx+(A_2\rho_2 u_2^2-A_1\rho_1 u_1^2) \\
& =-(A_2p_2-A_1p_1)+\int_{①}^{②}pdA \\
& =-(A_2p_2-A_1p_1)+\overline{p}(A_2-A_1)
\end{align*}
\] $$ただし、\overline{p}は平均圧力である。$$

左辺は単位時間当たりの運動量変化を、右辺は圧力による外力を表している。

定常かつ断面積変化がないとすると、

$$\rho_2u_2^2-\rho_1u_1^2=p_1-p_2$$

垂直衝撃波では、この式を用いる。

まとめページ

流体力学

流体力学連続方程式(質量保存則)の導出オイラーの運動方程式(直交座標・極座標)の導出流線の方程式と速度ポテンシャル・流れ関数の定義と関係式ベルヌーイの定理(エネルギー保存則)の導出流体の変形と回転・渦度と[…]