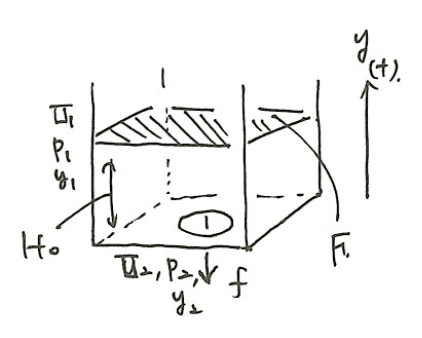
底面積Fの直方体の容器に液体が入っており、容器の底には面積fの孔があいている。
t=0で液面の高さがH0であるとすると、容器内の液体がすべて流出するのに必要な時間を求めよ。ただし、縮流効果は無視する。
(解)
ベルヌーイの式(非定常・非圧縮)を用いる。
$$\frac{1}{2}U^2+gy+\frac{p}{\rho}+\int\frac{\partial U}{\partial t}ds=const$$
いま、\(s\)軸は\(y\)軸に一致する。ある瞬間における、液面の流速、圧力、位置を\(U_1、p_1、y_1\)とし、孔でのそれらを\(U_2、p_2、y_2\)とする。ベルヌーイの式は
$$\frac{1}{2}U_1^2+gy_1+\frac{p_1}{\rho}+\int\frac{\partial U}{\partial t}dy=\frac{1}{2}U_2^2+gy+\frac{p_2}{\rho}+\int\frac{\partial U}{\partial t}dy$$
整理して
$$\frac{1}{2}(U_2^2-U_1^2)+g(y_2-y_1)+\frac{p_2-p_1}{\rho}+\int_{y_1}^{y_2}\frac{\partial U}{\partial t}dy=0$$
いま、液面は上下ともに大気に接しているので、\(p_1=p_2=p(大気圧)\)である。
$$\frac{1}{2}(U_2^2-U_1^2)+g(y_2-y_1)+\frac{dU}{dt}(y_2-y_1)=0 …①$$
さて、孔における流速は、液体粒子の自由落下(エネルギー保存則が成り立つ)と考えると
$$U_2=\sqrt{2gy_1}$$
とできる。さらに流量一定則
$$FU_1=fU_2$$
から、\(U_1\)が求められる。
$$U_1=\frac{f}{F}\sqrt{2gy_1}$$
\(y_2=0\)として、①を整理すると
$$\frac{1}{2}\left[U_2^2-\left(\frac{f}{F}\right)^2U_2^2\right]+(-gy_1)+\frac{dU}{dt}(-y_1)=0$$
$$\frac{dU}{dt}=-g\left(\frac{f}{F}\right)^2$$
$$U=-g\left(\frac{f}{F}\right)^2t+C_1 (C_1:積分定数)$$
\(t=0\)で\(y_1=H_0\)より、
$$U(0)=\frac{f}{F}\sqrt{2gH_0}=C_1$$
\(y\)軸は上向き正であることに注意すると、\(U=-dy_1/dt\)なので
$$-\frac{dy_1}{dt}=-g\left(\frac{f}{F}\right)^2t+\frac{f}{F}\sqrt{2gH_0}$$
$$-y_1=-\frac{g}{2}\left(\frac{f}{F}\right)^2t^2+\frac{f}{F}\sqrt{2gH_0}・t+C_2 (C_2:積分定数)$$
\(t=0\)で\(y_1=H_0\)より、
$$C_2=-H_0$$
よって、
$$\frac{g}{2}\left(\frac{f}{F}\right)^2t^2-\sqrt{2gH_0}\frac{f}{F}t+(H_0-y_1)=0$$
これは、\(t\)に関する二次方程式である。これを解いて
$$t=\frac{F}{f}\sqrt{\frac{2}{g}}(\sqrt{H_0}-\sqrt{y_1})$$
となる。
容器内の液体が空になるのは、\(y_1=0\)となるときなので、求める時間は
$$t=\frac{F}{f}\sqrt{\frac{2H_0}{g}}$$
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]





