さて、今回からはベクトル解析について学んでいきたいと思います。
まず、ベクトルの外積について考えます。そのあと、スカラー場とベクトル場を結ぶ重要な演算である勾配(grad)・発散(div)・回転(rot)の計算方法について述べ、それらの間に成り立つ公式を与えていきます。
ベクトル解析は力学や電磁気学をはじめ様々な分野で登場しますので、しっかり押さえておきましょう。
ベクトルの基本
Oを原点とするxyz座標系において、x軸、y軸、z軸方向の単位ベクトルをそれぞれ\(\mathbf{i}、\mathbf{j}、\mathbf{k}\)とします。これに順番をつけた組\(\{\mathbf{i},\mathbf{j},\mathbf{k}\}\)を、この座標系の関する基本ベクトルと呼びます。
\(\mathbf{i}\)から\(\mathbf{j}\)の向きに右ねじを回したときに、ねじが\(\mathbf{k}\)の向きに進むとき、この座標系は右手系であるといいます。
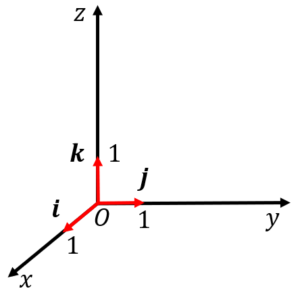
これ以降、右手系のxyz座標系について考えます。
ベクトルAの成分を\((A_x, A_y, A_z)\)、Aの長さを|A|とかきます。すなわち
$$\mathbf{A}=A_x\mathbf{i}+A_y\mathbf{j}+A_z\mathbf{k}$$
$$|\mathbf{A}|=\sqrt{A_x^2+A_y^2+A_z^2}$$
内積
ベクトル\(\mathbf{A}=(A_x, A_y, A_z)\)、\(\mathbf{B}=(B_x, B_y, B_z)\)の内積(スカラー積)を\(\mathbf{A}・\mathbf{B}\)とかき、
\[
\begin{align*}
\mathbf{A}・\mathbf{B}&=|\mathbf{A}||\mathbf{B}|\cos\theta \\
&=A_xB_x+A_yB_y+A_zB_z
\end{align*}
\]
と計算します。ここで、\(\theta\)は\(\mathbf{A}と\mathbf{B}\)のなす角で、\(0≦\theta≦\pi\)とします。
外積
\(\mathbf{A}と\mathbf{B}\)の外積(ベクトル積)\(\mathbf{A}×\mathbf{B}\)を、次のように定義します。
①大きさは\(\mathbf{A}、\mathbf{B}\)がつくる平行四辺形の面積に等しい
②方向は\(\mathbf{A}と\mathbf{B}\)のつくる平面に垂直で、\(\mathbf{A}\)から\(\mathbf{B}\)にねじを回すときにねじが進む向き
外積について、次のことが成り立ちます。
(1) \(\mathbf{A}と\mathbf{B}\)が平行であるとき、\(\mathbf{A}×\mathbf{B}=0\)
(2) \(\mathbf{B}×\mathbf{A}=-\mathbf{A}×\mathbf{B}\)
(3) \((\mathbf{A}+\mathbf{B})×\mathbf{C}=\mathbf{A}×\mathbf{C}+\mathbf{B}×\mathbf{C}\)
(4) \((a\mathbf{A})×\mathbf{B}=\mathbf{A}×(a\mathbf{B})=a(\mathbf{A}×\mathbf{B})\) (aは実数)
外積の計算は、順番を入れ換えない限り、内積と同様に行うことができます。
単位ベクトル間の外積の関係式
$$\mathbf{i}×\mathbf{i}=\mathbf{j}×\mathbf{j}=\mathbf{k}×\mathbf{k}=\mathbf{0}$$
$$\mathbf{i}×\mathbf{j}=\mathbf{k},\mathbf{j}×\mathbf{k}=\mathbf{i},\mathbf{k}×\mathbf{i}=\mathbf{j}$$
より、\(\mathbf{A}=(A_x, A_y, A_z)、\mathbf{B}=(B_x, B_y, B_z)\)に対して次を得ます。
$$\mathbf{A}×\mathbf{B}=(A_yB_z-B_yA_z)\mathbf{i}+(A_zB_x-B_zA_x)\mathbf{j}+(A_xB_y-B_xA_y)\mathbf{k}$$
スカラー場とベクトル場
空間内のある領域の各点に対して、スカラーが対応しているとき、この対応のことをスカラー場といいます。例えば、温度は空間中の各位置でスカラー量を持つため、温度分布はスカラー場となります。
これに対して、各点にベクトルが対応している場合をベクトル場といいます。例えば、ある位置における重力は方向と大きさが決まりますので、重力場はベクトル場です。
xyz座標系におけるある領域上のスカラー場またはベクトル場は、領域上で定義されたx, y, zの実数値関数\(f\)またはベクトル値関数\(\mathbf{A}\)として表されます。以降、\(f\)および\(\mathbf{A}\)は\(C^2\)級と仮定します。
勾配(gradient)
スカラー場\(f\)に対して、ある定数\(c\)を与えたとき、方程式\(f(x, y, z)=c\)は一般に曲面を表します。これを等位面と呼びます。
\(f\)に対し、次の演算を勾配と呼びます。
x, y, zの各方向に対する偏微分、すなわち傾きを表しています。
\(grad f\)はベクトル場です。
微分演算子∇
をナブラと呼び、形式的なベクトルとみなします。
これを用いると、スカラー場fに対して\(grad f\)はベクトル\(\nabla\)のスカラー倍と考えることができ
$$gradf=\nabla f$$
と表されます。
発散(divergence)、回転(rotation)
∇とベクトルの内積・外積を考えることができます。それぞれ発散・回転といい、次のように定義します。
\[
rot\mathbf{A}=\nabla×\mathbf{A}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k}\\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
A_x & A_y & A_z
\end{array}\right| \\
=\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}\right)\mathbf{i}+\left(\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}\right)\mathbf{j}+\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\mathbf{k}
\]
これらの物理的意味については別記事で述べる予定にしています。
よく使う公式
以上の微分演算について成り立つ公式を挙げておきます。
$$div(rot\mathbf{A})=\nabla・(\nabla×\mathbf{A})=0$$
$$rot(gradf)=\nabla×\nabla f=0$$
$$\nabla・(\mathbf{A}×\mathbf{B})=(\nabla×\mathbf{A})・\mathbf{B}-\mathbf{A}・(\nabla×\mathbf{B})$$
$$\nabla×(\nabla×\mathbf{A})=\nabla(\nabla・\mathbf{A})-\Delta\mathbf{A}$$
$$ただし、\Delta=\nabla・\nabla=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$$
Δをラプラシアンと呼びます。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




