今回から数回にわたって、曲線についての学習をしていきます。
第一回のこの記事では、まず空間中の曲線をベクトルによって表示し、その微分の定義と意味合い、ベクトルの微分公式について書いていきます。
空間曲線の表し方
$$閉区間[\alpha ,\beta]上の連続関数x=x(t), y=y(t), z=z(t)により得られる点$$
$$P(t)=(x(t),y(t),z(t))$$
$$の軌跡Cを空間曲線といい、tを媒介変数またはパラメータと呼ぶ$$

空間上の曲線は、空間中の点が作り出す軌跡として表現することができます。空間中の点はx,y,zの各座標の値を指定することで位置を確定することができます。x,y,zそれぞれを個別の関数とするよりも、ひとつの変数で統一的に表しておくことで便利に取り扱うことができます。
$$点P(\alpha)をCの始点、P(\beta)を終点と呼び、始点と終点が一致する曲線を閉曲線と呼ぶ。$$
空間中の点は、原点Oを基準とする位置ベクトルで表すことができます。
$$曲線C:\mathbf{r}=\mathbf{r}(t)とかくことにする。\mathbf{r}(t)はx(t),y(t),z(t)を成分にもつベクトルで、$$
$$点P(t)の位置ベクトルを表す。\mathbf{r}(t)は[\alpha ,\beta]上のベクトル値関数となる$$
ベクトルの微分
空間中の曲線をベクトルで表すことにしました。曲線の特徴を取り扱うために微分を活用するために、ベクトルの微分について考えておく必要があります。
ベクトルの収束
$$ベクトル値関数\mathbf{r}(t)について、|\mathbf{r}(t)-\mathbf{b}| \to 0 (t\to t_1)となる定ベクトル$$
$$\mathbf{b}=(b_1, b_2, b_3)が存在するとき、t\to t_1のとき\mathbf{r}(t)は\mathbf{b}に収束する、といい次のように書く$$
$$\lim_{t\to t_1} \mathbf{r}(t)=\mathbf{b} または \mathbf{r}(t)\to \mathbf{b} (t\to t_1)$$
ベクトルの連続
$$t\to t_1のとき、\mathbf{r}(t)\to \mathbf{r}(t_1)ならば\mathbf{r}=\mathbf{r}(t)はt\to t_1で連続であるという$$
$$定義域の各点で連続であるとき、\mathbf{r}(t)は連続であるという$$
微分
ベクトル値関数の微分を考えます。
$$\lim_{\Delta t\to 0} \frac{\mathbf{r}(t+\Delta t)-\mathbf{r}(t)}{\Delta t}$$
$$が存在するとき、この極限を\mathbf{r}(t)の微分係数と呼ぶ。各点で微分係数をもつとき、$$
$$\mathbf{r}=\mathbf{r}(t)は微分可能であるといい、その導関数を\frac{d\mathbf{r}}{dt}とかく$$
$$\mathbf{r}=\mathbf{r}(t)が微分可能となるのは、各成分が微分可能であるときで$$
$$\frac{d\mathbf{r}}{dt}=\left( \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \right)$$
ベクトル値関数の微分は、各成分の関数の微分として与えられます。1変数関数の微分と大きく変わることはありませんね。
1変数関数の微分で出てきた用語をベクトル値関数にも同様に当てはめていきます。
$$\mathbf{r}(t)のn階導関数が存在し、それらがすべて連続であるとき\mathbf{r}(t)はC^n級であるという$$
特異点と正則
$$C^1級の曲線C:\mathbf{r}=\mathbf{r}(t)について、\frac{d\mathbf{r}}{dt}=\mathbf{0}を満たす点P(t)を特異点と呼ぶ$$
$$特異点でない点を正則点と呼び、特異点を持たない曲線を正則曲線と呼ぶ$$
特異点P(t)は、曲線が滑らかではない点のことを表しています。特異点の例として、孤立した点や曲線がとがっている点などがあります。
速度ベクトルと加速度ベクトル
ベクトルの微分の物理的意味について考えていきます。
$$以降この節ではC:\mathbf{r}=\mathbf{r}(t)をC^2級の正則曲線とし、\frac{d\mathbf{r}}{dt}、\frac{d^2\mathbf{r}}{dt^2}を\dot{\mathbf{r}}、\ddot{ \mathbf{r}}とかく$$
導関数を分数形で表す方式はライプニッツ流の表記、上にドットを付けて表す方式はニュートン流の表記です。ニュートンが確立した力学の分野では特に後者の表記法を用いることが多いです。
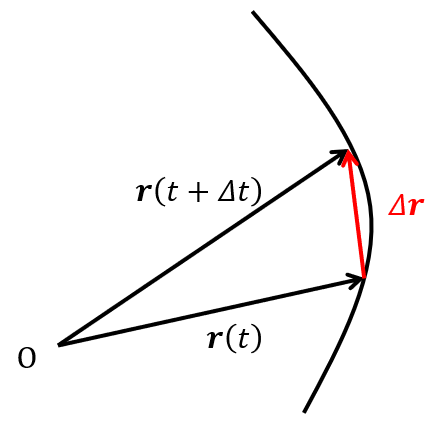
$$\dot{\mathbf{r}}は曲線Cの接線ベクトルを表す。このことは、$$
$$\frac{\Delta \mathbf{r}}{\Delta t}=\frac{\mathbf{r}(t+\Delta t)-\mathbf{r}(t)}{\Delta t}$$
$$において\frac{\Delta \mathbf{r}}{\Delta t}が\Delta \mathbf{r}と同じ方向のベクトルであることからわかる$$
$$\dot{\mathbf{r}}を単位化してできるベクトル\frac{\dot{\mathbf{r}}}{|\dot{\mathbf{r}}|}を単位接線ベクトルとよび、\mathbf{t}で表す$$
パラメータtを時間を表す変数ととらえると、曲線Cは空間中を運動する質点の軌跡と見ることができます。
すると、「位置ベクトルrの時間微分」は、「ある時刻における位置の瞬間的な変化すなわち速度」を表すことが分かります。さらに「速度の時間微分」は「速度の瞬間的な変化すなわち加速度」を表します。
$$\mathbf{v}=\dot{\mathbf{r}}=(\dot{x},\dot{y},\dot{z})を速度ベクトル、\mathbf{a}=\ddot{\mathbf{r}}=(\ddot{x},\ddot{y},\ddot{z})を加速度ベクトルと呼ぶ$$






