正方行列について定義される行列式は逆行列を求める場合などに用いられる重要な量である。
2次の行列であればその行列式は容易に計算することができるが、3次以上になると計算量が多く複雑になってしまう。
ここでは、3次正方行列の行列式の求め方を簡単に覚える方法である「サラスの公式」(サラスの方法やサラスの規則とも呼ぶ)を紹介する。
3次正方行列の行列式
3次正方行列\(A\)
\[A=\left(
\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right)\]
の行列式は
\[\begin{align*} \mathrm{det}(A) = |A| &= \left|
\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right| \\ &=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} \\ &~~~~~-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}
\end{align*}\]
で与えられる。
一見複雑な行列式の計算だが、実はある法則がある。
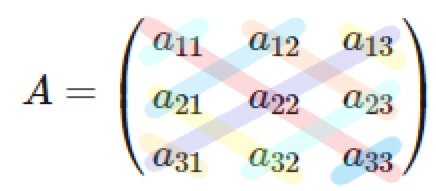
図のように、左上から右下に向かう3成分の積はプラス、右上から左下に向かう3成分の積はマイナスですべて足し合わせる。
オレンジや黄色の線のように途中で行列の外に出てしまう場合は、反対側から出てくる”魔方陣”のようなイメージを持つとよい。
このような方法を、サラスの公式という。
例題を用いて使い方を理解しよう。
例題
次の行列の行列式を計算せよ。
\[(1) A=\left(
\begin{array}{ccc}
1 & 2 & 3 \\
2 & 4 & 5 \\
3 & 5 & 6
\end{array}
\right) , (2) B=\left(
\begin{array}{ccc}
a & b & c \\
c & a & b \\
b & c & a
\end{array}
\right)\]
(解)
(1)
\[\begin{align*}|A|&=\left|
\begin{array}{ccc}
1 & 2 & 3 \\
2 & 4 & 5 \\
3 & 5 & 6
\end{array}
\right| \\ &=1\times4\times6+2\times5\times3+3\times2\times5 \\ &~~~~~-3\times4\times3-2\times2\times6-1\times5\times5 \\ &=24+30+30-36-24-25 \\&=-1
\end{align*}\]
(2)
\[\begin{align*}|B|&=\left|
\begin{array}{ccc}
a & b & c \\
c & a & b \\
b & c & a
\end{array}
\right| \\ &=a^3+b^3+c^3-3abc \\ &=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)
\end{align*}\]
次を満たす\(x\)の値を求めよ。
\[\left|
\begin{array}{ccc}
1-x & 0 & -1 \\
1 & 2-x & 1 \\
2 & 2 & 3-x
\end{array}
\right|=0\]
(解)
\[\begin{align*}\left|
\begin{array}{ccc}
1-x & 0 & -1 \\
1 & 2-x & 1 \\
2 & 2 & 3-x
\end{array}
\right| &=(1-x)(2-x)(3-x)-2+2(2-x)-2(1-x)\\&=(1-x)(2-x)(3-x)=0
\end{align*}\]
$$∴x=1,2,3$$
計算量は多いが、丁寧に行えば難しくはないことがお分かりいただけただろうか。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




