ここからは偏微分の応用の話に入ります。
まずは、偏微分を用いて空間中の曲面の特徴について調べていきましょう。
曲面
偏微分係数\(f_x(a,b)\)は、定義より
$$f_x(a,b)=\left. \frac{d}{dx}f(x,b)\right|_{x=a}$$
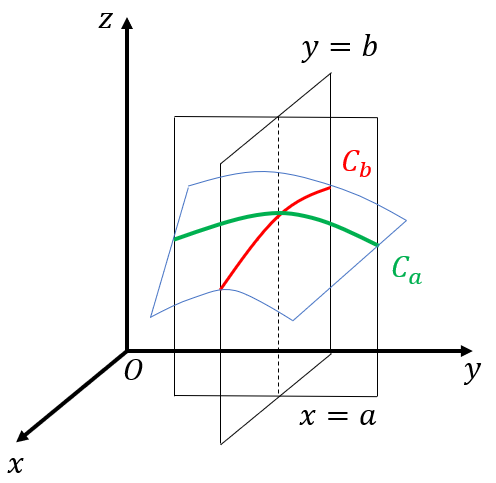
曲面\(S\)の、平面\(y=b\)による切り口に現れる曲線を\(C_b\)とすると、\(f_x(a,b)\)は\(C_b\)の\(x=a\)における接線の\(xy\)-平面に対する傾きと等しくなります。
同様に、\(S\)の平面\(x=a\)による切り口の曲線を\(C_a\)とすると、\(f_y(a,b)\)は\(C_a\)の\(y=b\)における接線の\(xy\)-平面に対する傾きに等しくなります。
方向微分係数
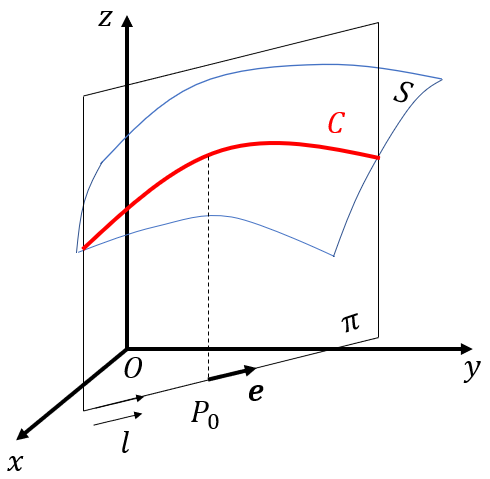
\(xy\)-平面上に単位ベクトル\(\mathbf{e}=(\lambda, \mu)\)と、点\(P_0(a, b)\)を通り\(\mathbf{e}\)を方向ベクトルとする有向直線\(l\)を考えます。
\(l\)上の点\(P\)をとり、
$$\overrightarrow{P_0P}=t\mathbf{e}$$
とおきます。このとき、極限値
$$\lim_{t\to0}\frac{f(P)-f(P_0)}{t}$$
が存在する場合、この値を\(f(x, y)\)の\(P_0\)における\(\mathbf{e}\)方向微分係数と呼びます。
すなわち、直線\(l\)を含み\(xy\)-平面に垂直な平面を\(\pi\)、\(S\)の\(\pi\)による切り口の曲線を\(C\)とすると、\(f(x, y)\)の\(P_0\)における\(\mathbf{e}\)方向微分係数は\(C\)の点\((a, b, f(a, b))\)における接線の\(xy\)-平面に対する傾きに等しくなります。
関数\(f(x, y)\)が\(P_0(a, b)\)で全微分可能であるとします。
$$P(a+\lambda t, b+\mu t),\lambda^2+\mu^2=1$$
から
とおけるので、
$$\lim_{t\to0}\frac{f(P)-f(P_0)}{t}=f_x(P_0)\lambda+f_y(P_0)\mu$$
この右辺は、ベクトル\((f_x(P_0), f_y(P_0))\)と\(\mathbf{e}\)の内積に等しいことがわかります。
一般に、全微分可能な関数\(f(x, y)\)に対して\((∂f/∂x, ∂f/∂y)\)を成分に持つベクトル値関数をfの勾配(gradient)とよび、\(\mathrm{grad}f\)で表します。
定理:方向微分係数
関数\(f(x,y)\)が\(P_0(a,b)\)で全微分可能であるならば、すべての方向に微分可能であり
単位ベクトル\(\mathbf{e}\)方向の微分係数は次式で与えられる。
$$内積 \mathrm{grad}f(P_0)・\mathbf{e}$$
法線ベクトルと接平面
3変数関数\(\phi(x, y, z)\)に対しても、勾配
$$\mathrm{grad}\phi=\left(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z} \right)$$
を定義します。\(\phi(x, y, z)=0\)で表される図形Sは、\(\phi(x, y, z)\)が\(C^1\)級でS上\(\mathrm{grad}\phi≠0\)であるとき、滑らかな曲線であるといいます。
\(P_0∈S\)とすると、仮定より\(\mathrm{grad}\phi(P_0)\)のある成分は0ではありません。
たとえば\(\phi_z(P_0)≠0\)とすると、陰関数定理により\(P_0\)の近くではSは\(C^1\)級関数なので\(z=f(x, y)\)と表されることから、曲面を表していることがわかります
いま、S上の点\(P_0\)をとり、\(P_0\)を通るS上の任意の曲線
$$C:\mathbf{r}(t)=(x(t),y(t),z(t))$$
を考えます。CはS上にあるので、\(\phi(x(t),y(t),z(t))=0\)です。この両辺をtで微分すると、
$$\phi_xx'(t)+\phi_yy'(t)+\phi_zz'(t)=0$$
\(t=t_0\)が\(P_0\)に対応するとして代入すると
$$\mathrm{grad}\phi(P_0)・\mathbf{r}'(t_0)=0$$
となります。これは、ベクトル\(\mathrm{grad}\phi(P_0)\)がCの\(P_0\)における接ベクトル\(\mathbf{r}'(t)\)と直交することを示しています。
したがって、ベクトル\(\mathrm{grad}\phi(P_0)\)は\(P_0\)を通るS上の任意の曲線と\(P_0\)において直交します。
\(P_0(a, b, c)\)としたとき、接平面の方程式は次のように表されます。
$$\phi_x(P_0)(x-a)+\phi_y(P_0)(y-b)+\phi_z(P_0)(z-c)=0$$
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




