複素速度ポテンシャルを用いると、流れの様子を解析することができる。
この複素速度ポテンシャルと写像の関係式を用いて、複雑な流れ場の解析に応用していく。
ζ平面の複素速度ポテンシャル
z平面からζ平面への写像を行ったときの、複素速度ポテンシャルと共役複素速度を計算する。
ζ平面の複素速度ポテンシャルF(ζ)が
$$F(\zeta)=\phi(\xi,\eta)+i\psi(\xi,\eta)$$
と与えられたとき、z=f(ζ)およびζ=g(z)より、z平面での複素速度ポテンシャルは、G(z)=F(g(z))で与えられる。したがって
$$\frac{dG(z)}{dz}=\frac{dF(g(z))}{dg(z)}・\frac{dg(z)}{dz}=\frac{dF(\zeta)}{d\zeta}・\frac{d\zeta}{dz}$$
から、共役複素速度が求まる。逆に、z平面からζ平面への写像の場合は
$$\frac{dF(\zeta)}{d\zeta}=\frac{dG(z)}{dz}・\frac{dz}{d\zeta}$$
より求まる。
具体例で確認していく。
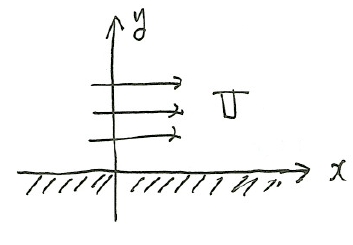
(1)直角壁を曲がる流れ
は、\(F(z)=Uz\)である。
これを、\(\zeta=\sqrt{z}\)の関係式でζ平面に写像する。\(z=\zeta^2\)より、
$$x+iy=(\xi+i\eta)^2$$
$$x=\xi^2-\eta^2 ,y=2\xi\eta$$
ここで、点\((x, 0)\)が写る先を考える。\(x_0\ge 0\)として
$$(x_0,0) \to \xi_0=\sqrt{x_0} / (-x_0,0) \to \eta_0=\sqrt{x_0}$$
よって、\(x\ge0\)は\(\xi\ge0\)へ、\(x\le0\)は\(\eta\ge0\)へと壁が写る。
次に複素速度ポテンシャルは
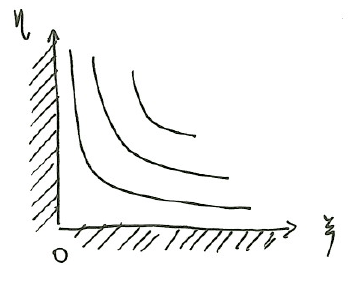
$$G(\zeta)=F(z)=F(\zeta^2)=U\zeta^2=U(\xi^2-\eta^2)+i・2U\xi\eta=\phi+i\psi$$
となり、\(\psi=const\)の流線は、\(\xi\eta=const\)より直角双曲線を表す。図示すると下のようになる。
共役複素速度は、
$$\frac{dG}{d\zeta}=2U\zeta=2U\xi+i2U\eta$$
となる。したがって
\[
\begin{cases}
\xi方向の分速度: 2U\xi \\
\eta方向の分速度: -2U\eta
\end{cases}
\]
(2)楕円周りの流れ
円柱周りの流れは、一様流と2重吹き出しの組み合わせで記述することができる。(参考)
半径rの円柱まわりの複素速度ポテンシャルは、次式で与えられる。
$$F(\zeta)=U\left(\zeta+\frac{r^2}{\zeta}\right)$$
\(\zeta=\xi+i\eta\)とすると
$$F(\zeta)=U\xi\left(1+\frac{r^2}{\xi^2+\eta^2}\right)+iU\eta\left(1-\frac{r^2}{\xi^2+\eta^2}\right)$$
よって、\(\psi=0\)となる流線は
$$\xi^2+\eta^2=r^2 or \eta=0$$
さて、この流れのジューコフスキー写像(\(z=\zeta+a^2/\zeta (a\lt r)\))を計算する。
\(\zeta=re^{i\theta}\)として
$$z=re^{i\theta}+a^2e^{-i\theta}=\left(r+\frac{a^2}{r}\right)\cos\theta+i\left(r-\frac{a^2}{r}\right)\sin\theta$$
よって
$$x=\left(r+\frac{a^2}{r}\right)\cos\theta=A\cos\theta ,y=\left(r-\frac{a^2}{r}\right)\sin\theta=B\sin\theta$$
これは、長軸\(A\)、短軸\(B\)の楕円を表す。焦点は\((\pm\sqrt{A^2-B^2}, 0)=(\pm2a, 0)\)である。
いま、\(dz/d\zeta=1-a^2/\zeta^2\)より、\(\zeta=\pm a\)では\(dz/d\zeta=0\)となり特異点である。よって、\(\zeta=\pm a\)を除き等角写像可能であり、\(r\gt a\)で考えればよい。
次に、共役複素速度は
$$\frac{dG(z)}{dz}=\frac{dF(\zeta)}{d\zeta}・\frac{d\zeta}{dz}=U\left(1-\frac{r^2}{\zeta^2}\right)/\left(1-\frac{a^2}{\zeta^2}\right)$$
\(\zeta=re^{i\theta} (r>a)\)として
$$u-iv=U\frac{1-\cos 2\theta-i\sin 2\theta}{1-\left(\frac{a}{r}\right)^2\cos 2\theta+i\left(\frac{a}{r}\right)^2\sin 2\theta}$$
これは、一様流(流速:\(U\))の中に楕円柱を長軸と\(U\)が平行にあるように置いたときの共役複素速度である。
長軸の両端\((\theta=0, \pi)\)では、\(u-iv=0\)なので、\(u=v=0\)である。すなわち、ここはよどみ点になる。
短軸の両端\((\theta=\pi/2, 3\pi/2)\)では、
$$u-iv=\frac{2U}{1-\left(\frac{a}{r}\right)^2}$$
$$u=\frac{2U}{1-\left(\frac{a}{r}\right)^2} ,v=0$$
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]